Influence of Operating and Electrochemical Parameters on PEMFC Performance: A Simulation Study
Abstract
:1. Introduction
2. Model Development
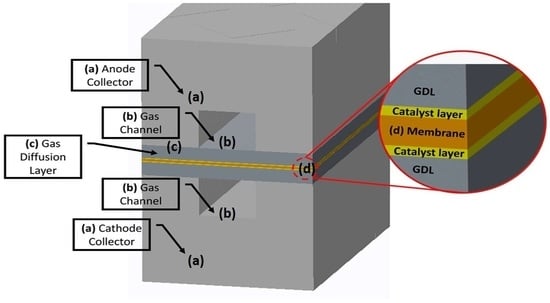
2.1. Geometry, Mesh, and Other Parameters
2.2. Boundary Conditions
- The mass flow inlet as a boundary type is used at inlets of both the anode and cathode sides. The values of temperature, mass flow rate, and mass fraction of hydrogen, oxygen, nitrogen gases, and water are prescribed;
- At the outlets on both sides of the anode and cathode, the boundary condition is the pressure outlet used. While the value of pressure is prescribed and the options of backflow conditions are defined;
- The stationary wall type shall be set as a wall region between outlets and inlets;
- There is zero flux boundary condition for a membrane phase potential on all outside boundaries because no photonic current leaves the fuel cell through an external boundry;
- On external contact boundaries, the values of solid potential are fixed as potential static boundary conditions. In this model, the solid phase potential is fixed as the potential on the anode side and on the cathode side are set to zero. The solid-phase potential is set to the cell voltage.
2.3. Model Validation
2.4. Model Assumptions
3. Governing Equation
4. Results and Discussion
4.1. Effect of Temperature
4.2. Effect of Operating Pressure
4.3. Effect of Anode- and Cathode-Relative Humidification
4.4. Effect of Exchange Coefficient
4.5. Effect of RCD
4.6. Effect of GDL Porosity
4.7. Effects of Electrochemical Parameters at Non-Isothermal Conditions
4.8. Effect of GDL Porosity on Exchange Coefficient
| Paramters | Anode Value | Cathode Value | Ref. |
|---|---|---|---|
| RCD (A/m3) | 3750, 7500, 15,000, 22,500 | 10, 20, 30, 40 | Assumed |
| Exchange coefficient | 0.5, 1, 1.5, 2 | 0.5, 1, 1.5, 2 | Assumed |
| Pressure (atm) | 1, 2, 3, 4 | 1, 2, 3, 4 | [39] |
| Temperature (K) | 323, 333, 343, 353 | 323, 333, 343, 353 | [39] |
| Relative humidity | 25%, 50%, 75%, 100% | 25%, 50%, 75%, 100% | [42] |
| GDL porosity | 0.2, 0.4, 0.6, 0.8 | 0.2, 0.4, 0.6, 0.8 | [45] |
| Concentration exponent | 0.5 | 1 | [48] |
| Reference concentration (K mol/m3) | 1 | 1 | [48] |
| CL porosity | 0.5 | 0.5 | [48] |
| Mass flow rate H2 (Kg/s) | 6.0 × 10−7 | 5.0 × 10−6 | [48] |
| Open circuit voltage (V) | 0.95 | 0.95 | [48] |
| GDL porosity | 0.2, 0.4, 0.6, 0.8 | 0.2, 0.4, 0.6, 0.8 | [49] |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Future work and recommendations
References
- Qian, X.; Chen, L.; Yin, L.; Liu, Z.; Pei, S.; Li, F.; Hou, G.; Chen, S.; Song, L.; Thebo, K.H.; et al. CdPS3 nanosheets-based membrane with high proton conductivity enabled by Cd vacancies. Science 2020, 370, 596–600. [Google Scholar] [CrossRef] [PubMed]
- Peera, S.G.; Maiyalagan, T.; Liu, C.; Ashmath, S.; Lee, T.G.; Jiang, Z.; Mao, S. A review on carbon and non-precious metal based cathode catalysts in microbial fuel cells. Int. J. Hydrogen Energy 2021, 46, 3056–3089. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.; Elsaid, K.; Wilberforce, T.; Kamil, M.; Sayed, E.T.; Olabi, A. Environmental aspects of fuel cells: A review. Sci. Total Environ. 2021, 752, 141803. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.; Zhang, C.; Ling, C.-Y.; Han, M.; Yong, R.-Y.; Sun, D.; Chen, J. Review on current research of materials, fabrication and application for bipolar plate in proton exchange membrane fuel cell. Int. J. Hydrogen Energy 2020, 45, 29832–29847. [Google Scholar] [CrossRef]
- Mustain, W.E.; Chatenet, M.; Page, M.; Kim, Y.S. Durability challenges of anion exchange membrane fuel cells. Energy Environ. Sci. 2020, 13, 2805–2838. [Google Scholar] [CrossRef]
- Hussain, S.; Li, Y.; Mustehsin, A.; Ali, A.; Thebo, K.H.; Ali, Z.; Hussain, S. Synthesis and characterization of ZnO/samarium-doped ceria nanocomposites for solid oxide fuel cell applications. Ionics 2021, 27, 4849–4857. [Google Scholar] [CrossRef]
- Hussain, S.; Li, Y.; Thebo, K.H.; Ali, Z.; Owais, M.; Hussain, S. Effect of iron oxide co-doping on structural, thermal, and electrochemical properties of samarium doped ceria solid electrolyte. Mater. Chem. Phys. 2021, 267, 124576. [Google Scholar]
- Hussain, S.; Li, Y.; Memon, F.H.; Hussain, S.; Li, L.; Thebo, K.H. Studies on the effects of pre-firing and sintering temperature on NSDC nanocomposite electrolytes. Prog. Nat. Sci. Mater. Int. 2022, 32, 128–134. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, Y.; Xu, Y.; Guo, X.; Cao, Y.; Ming, W. Modeling and Simulation of Membrane Electrode Material Structure for Proton Exchange Membrane Fuel Cells. Coating 2022, 12, 1145. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, X.; Zhang, T.; Pei, P. The reactant starvation of the proton exchange membrane fuel cells for vehicular applications: A review. Energy Convers. Manag. 2019, 182, 282–298. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, P.; Chen, H.; Pei, P. A review of automotive proton exchange membrane fuel cell degradation under start-stop operating condition. Appl. Energy 2018, 223, 249–262. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Su, X.; Wack, M.; Wu, L. Disturbance-Observer-Based Control for Air Management of PEM Fuel Cell Systems via Sliding Mode Technique. IEEE Trans. Control Syst. Technol. 2019, 27, 1129–1138. [Google Scholar] [CrossRef]
- Sun, L.; Shen, J.; Hua, Q.; Lee, K.Y. Data-driven oxygen excess ratio control for proton exchange membrane fuel cell. Appl. Energy 2018, 231, 866–875. [Google Scholar] [CrossRef]
- Li, J.; Chen, M.; Cullen, D.A.; Hwang, S.; Wang, M.; Li, B.; Liu, K.; Karakalos, S.; Lucero, M.; Zhang, H.; et al. Atomically dispersed manganese catalysts for oxygen reduction in proton-exchange membrane fuel cells. Nat. Catal. 2018, 1, 935–945. [Google Scholar] [CrossRef]
- Roshandel, R.; Farhanieh, B.; Saievar-Iranizad, E. The effects of porosity distribution variation on PEM fuel cell performance. Renew. Energy 2005, 30, 1557–1572. [Google Scholar] [CrossRef]
- Du, L.; Prabhakaran, V.; Xie, X.; Park, S.; Wang, Y.; Shao, Y. Low-PGM and PGM-Free Catalysts for Proton Exchange Membrane Fuel Cells: Stability Challenges and Material Solutions. Adv. Mater. 2021, 33, 1908232. [Google Scholar] [CrossRef]
- Sun, L.; Jin, Y.; You, F. Active disturbance rejection temperature control of open-cathode proton exchange membrane fuel cell. Appl. Energy 2020, 261, 114381. [Google Scholar] [CrossRef]
- Sohani, A.; Naderi, S.; Torabi, F.; Sayyaadi, H.; Akhlaghi, Y.G.; Zhao, X.; Talukdar, K.; Said, Z. Application based multi-objective performance optimization of a proton exchange membrane fuel cell. J. Clean. Prod. 2020, 252, 119567. [Google Scholar] [CrossRef]
- Li, X.; Ma, H.; Wang, P.; Liu, Z.; Peng, J.; Hu, W.; Jiang, Z.; Liu, B.; Guiver, M.D. Highly Conductive and Mechanically Stable Imidazole-Rich Cross-Linked Networks for High-Temperature Proton Exchange Membrane Fuel Cells. Chem. Mater. 2020, 32, 1182–1191. [Google Scholar] [CrossRef]
- Wang, C.-Y. Fundamental models for fuel cell engineering. Chem. Rev. 2004, 104, 4727–4766. [Google Scholar] [CrossRef] [PubMed]
- Pinto, A.M.; Oliveira, V.S.; Falcão, D.S.C. Direct Alcohol Fuel Cells for Portable Applications: Fundamentals, Engineering and Advances, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 9780128118986. [Google Scholar]
- Ramshaw, J.D. Elements of computational fluid dynamics. World Sci. 2011, 2, 140. [Google Scholar] [CrossRef]
- Iranzo, A.; Munoz, M.; Rosa, F.; Pino, J. Numerical model for the performance prediction of a PEM fuel cell. Model results and experimental validation. Int. J. Hydrogen Energy 2010, 35, 11533–11550. [Google Scholar] [CrossRef]
- Hashemi, F.; Rowshanzamir, S.; Rezakazemi, M. CFD simulation of PEM fuel cell performance: Effect of straight and serpentine flow fields. Math. Comput. Model. 2012, 55, 1540–1557. [Google Scholar] [CrossRef]
- Wang, H.; Sweikart, M.A.; Turner, J.A. Stainless steel as bipolar plate material for polymer electrolyte membrane fuel cells. J. Power Sources 2003, 115, 243–251. [Google Scholar] [CrossRef]
- Yuan, X.; Zeng, X.; Zhang, H.-J.; Ma, Z.-F.; Wang, C.-Y. Improved performance of proton exchange membrane fuel cells with p-toluenesulfonic acid-doped Co-PPy/C as cathode electrocatalyst. J. Am. Chem. Soc. 2010, 132, 1754–1755. [Google Scholar] [CrossRef]
- Iranzo, A.; Boillat, P.; Salva, A.; Biesdorf, J. PEM fuel cell operation under air and O2 feed: Analysis of cell performance and liquid water distributions. Fuel Cells 2016, 16, 463–468. [Google Scholar] [CrossRef]
- Xu, Y.; Peng, L.; Yi, P.; Lai, X. Numerical investigation of liquid water dynamics in wave-like gas channels of PEMFCs. Int. J. Energy Res. 2019, 43, 1191–1202. [Google Scholar] [CrossRef]
- Sadiq Al-Baghdadi, M.A.R. Three-dimensional computational fluid dynamics model of a tubular-shaped PEM fuel cell. Renew. Energy 2008, 33, 1334–1345. [Google Scholar] [CrossRef]
- Ming, W.; Sun, P.; Zhang, Z.; Qiu, W.; Du, J.; Li, X.; Zhang, Y.; Zhang, G.; Liu, K.; Wang, Y.; et al. A systematic review of machine learning methods applied to fuel cells in performance evaluation, durability prediction, and application monitoring. Int. J. Hydrogen Energy 2023, 48, 5197–5228. [Google Scholar] [CrossRef]
- Agodzińska, K.; Jönsson, P.G.; Yang, W. Pyrolysis and in-line catalytic decomposition of excavated landfill waste to produce carbon nanotubes and hydrogen over Fe- and Ni-based catalysts—Investigation of the catalyst type and process temperature. J. Chem. Eng. 2022, 446, 136808. [Google Scholar] [CrossRef]
- Zhao, J.; Tu, Z.; Chan, S.H. In-situ measurement of humidity distribution and its effect on the performance of a proton exchange membrane fuel cell. Energy 2022, 239, 122270. [Google Scholar] [CrossRef]
- Fu, X.; Gao, R.; Jiang, G.; Li, M.; Luo, D.; Hu, Y.; Yuan, Q.; Huang, W.; Zhu, N.; Yang, L.; et al. Evolution of atomic-scale dispersion of FeNx in hierarchically porous 3D air electrode to boost the interfacial electrocatalysis of oxygen reduction in PEMFC. Nano Energy 2021, 83, 105734. [Google Scholar] [CrossRef]
- Zhang, G.; Jiao, K. Multi-phase models for water and thermal management of proton exchange membrane fuel cell: A review. J. Power Sources 2018, 391, 120–133. [Google Scholar] [CrossRef]
- Liu, Z.; Mao, Z.; Wang, C.; Zhuge, W.; Zhang, Y. Numerical simulation of a mini PEMFC stack. J. Power Sources 2006, 160, 1111–1121. [Google Scholar] [CrossRef]
- Mahdavi, A.; Ranjbar, A.A.; Gorji, M.; Rahimi-Esbo, M. Numerical simulation based design for an innovative PEMFC cooling flow field with metallic bipolar plates. Appl. Energy 2018, 228, 656–666. [Google Scholar] [CrossRef]
- Aiyejina, A.; Sastry, M. PEMFC flow channel geometry optimization: A review. J. Fuel Cell Sci. Technol. 2012, 9, 011011. [Google Scholar] [CrossRef]
- Ahmadi, N.; Ahmadpour, V.; Rezazadeh, S. Numerical investigation of species distribution and the Anode transfer coefficient effect on the proton exchange membrane fuel cell (PEMFC) performance. Heat Transf. Res. 2015, 46, 71. [Google Scholar] [CrossRef]
- Wang, L.; Husar, A.; Zhou, T.; Liu, H. A parametric study of PEM fuel cell performances. Int. J. Hydrogen Energy 2003, 28, 1263–1272. [Google Scholar] [CrossRef]
- Al-Baghdadi, M.A.S.; Al-Janabi, H.A.S. Modeling optimizes PEM fuel cell performance using three-dimensional multi-phase computational fluid dynamics model. Energy Convers. Manag. 2007, 48, 3102–3119. [Google Scholar] [CrossRef]
- Barbir, F. PEM Fuel Cells: Theory and Practice, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 9780123983725. [Google Scholar]
- Falcão, D.; Pinho, C.; Pinto, A. Water management in PEMFC: 1-D model simulations. Cienc. Tecnol. Mater. 2016, 28, 81–87. [Google Scholar] [CrossRef]
- Cheng, S.-J.; Miao, J.-M.; Wu, S.-J. Investigating the effects of operational factors on PEMFC performance based on CFD simulations using a three-level full-factorial design. Renew. Energy 2012, 39, 250–260. [Google Scholar] [CrossRef]
- Kumar, A.; Reddy, R.G. Modeling of polymer electrolyte membrane fuel cell with metal foam in the flow-field of the bipolar/end plates. J. Power Sources 2003, 114, 54–62. [Google Scholar] [CrossRef]
- Sadeghifar, H.; Djilali, N.; Bahrami, M. Effect of Polytetrafluoroethylene (PTFE) and micro porous layer (MPL) on thermal conductivity of fuel cell gas diffusion layers: Modeling and experiments. J. Power Sources 2014, 248, 632–641. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A.; McDonald, M.S. Fuel Cell Systems Explained, 2nd ed.; John and Wiley and Sons: Chichester, UK, 2003. [Google Scholar]
- Soderberg, J.N.; Co, A.C.; Sirk, A.H.; Birss, V.I. Impact of porous electrode properties on the electrochemical transfer coefficient. J. Phys. Chem. B 2006, 110, 10401–10410. [Google Scholar] [CrossRef]
- Lau, C.N.; Bao, W.; Velasco, J., Jr. Properties of suspended graphene membranes. Mater. Today 2012, 15, 238–245. [Google Scholar] [CrossRef]
- Mortazavi, M.; Santamaria, A.D.; Chauhan, V.; Benner, J.Z.; Heidari, M.; Médici, E.F. Effect of PEM fuel cell porous media compression on in-plane transport phenomena. J. Power Sources Adv. 2020, 1, 100001. [Google Scholar] [CrossRef]










| Part | Length (mm) | Width (mm) | Height (mm) |
|---|---|---|---|
| GDL | 25 | 6 | 0.3 |
| CL | 25 | 6 | 0.02 |
| Membrane | 25 | 6 | 0.15 |
| Channels | 25 | 2 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soomro, I.A.; Memon, F.H.; Mughal, W.; Khan, M.A.; Ali, W.; Liu, Y.; Choi, K.H.; Thebo, K.H. Influence of Operating and Electrochemical Parameters on PEMFC Performance: A Simulation Study. Membranes 2023, 13, 259. https://doi.org/10.3390/membranes13030259
Soomro IA, Memon FH, Mughal W, Khan MA, Ali W, Liu Y, Choi KH, Thebo KH. Influence of Operating and Electrochemical Parameters on PEMFC Performance: A Simulation Study. Membranes. 2023; 13(3):259. https://doi.org/10.3390/membranes13030259
Chicago/Turabian StyleSoomro, Imtiaz Ali, Fida Hussain Memon, Waqas Mughal, Muhammad Ali Khan, Wajid Ali, Yong Liu, Kyung Hyun Choi, and Khalid Hussain Thebo. 2023. "Influence of Operating and Electrochemical Parameters on PEMFC Performance: A Simulation Study" Membranes 13, no. 3: 259. https://doi.org/10.3390/membranes13030259