Calculation of Three-dimensional Energy Product for Isotropic Nd2Fe14B Magnet
Abstract
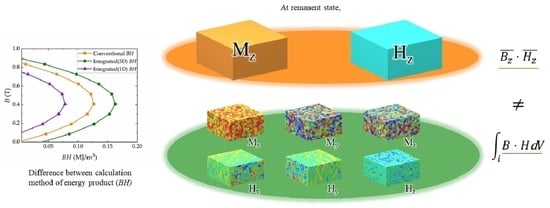
:1. Introduction
2. Materials and Methods
3. Simulation Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Coey, J.M.D. Perspective and Prospects for Rare Earth Permanent Magnets. Engineering 2020, 6, 119–131. [Google Scholar] [CrossRef]
- Cui, J.; Kramer, M.; Zhou, L.; Liu, F.; Gabay, A.; Hadjipanayis, G.; Balasubramanian, B.; Sellmyer, D. Current progress and future challenges in rare-earth-free permanent magnets. Acta Mater. 2018, 158, 118–137. [Google Scholar] [CrossRef]
- McCallum, R.W.; Lewis, L.; Skomski, R.; Kramer, M.J.; Anderson, I.E. Practical Aspects of Modern and Future Permanent Magnets. Annu. Rev. Mater. Res. 2014, 44, 451–477. [Google Scholar] [CrossRef]
- Coey, J.M.D. Magnetism and Magnetic Materials; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Kim, N.; Han, H.-S.; Lee, S.; Kim, M.-J.; Jung, D.-H.; Kang, M.; Ok, H.; Son, Y.; Lee, S.; Lee, K.-S. Geometric effects in cylindrical core/shell hard–soft exchange-coupled magnetic nanostructures. J. Magn. Magn. Mater. 2021, 523, 167599. [Google Scholar] [CrossRef]
- Skomski, R.; Coey, J.M.D. Magnetic anisotropy—How much is enough for a permanent magnet? Scr. Mater. 2016, 112, 3–8. [Google Scholar] [CrossRef] [Green Version]
- Forster, H.; Bertram, N.; Wang, X.; Dittrich, R.; Schrefl, T. Energy barrier and effective thermal reversal volume in columnar grains. J. Magn. Magn. Mater. 2003, 267, 69–79. [Google Scholar] [CrossRef]
- Ivanov, Y.P.; Vázquez, M.; Chubykalo-Fesenko, O. Magnetic reversal modes in cylindrical nanowires. J. Phys. D Appl. Phys. 2013, 46, 485001. [Google Scholar] [CrossRef] [Green Version]
- Landeros, P.; Allende, S.; Escrig, J.; Salcedo, E.; Altbir, D.; Vogel, E.E. Reversal modes in magnetic nanotubes. Appl. Phys. Lett. 2007, 90, 102501. [Google Scholar] [CrossRef] [Green Version]
- Raviolo, S.; Arciniegas Jaimes, D.M.; Bajales, N.; Escrig, J. Wave reversal mode: A new magnetization reversal mechanism in magnetic nanotubes. J. Magn. Magn. Mater. 2020, 497, 165944. [Google Scholar] [CrossRef]
- Leighton, B.; Pereira, A.; Escrig, J. Reversal modes in asymmetric Ni nanowires. J. Magn. Magn. Mater. 2012, 324, 3829–3833. [Google Scholar] [CrossRef]
- Skomski, R.; Ke, L.; Kramer, M.J.; Anderson, I.E.; Wang, C.Z.; Zhang, W.Y.; Shield, J.E.; Sellmyer, D.J. Cooperative and noncooperative magnetization reversal in alnicos. AIP Adv. 2017, 7, 056222. [Google Scholar] [CrossRef]
- Shield, J.E.; Zhou, J.; Aich, S.; Ravindran, V.K.; Skomski, R.; Sellmyer, D.J. Magnetic reversal in three-dimensional exchange-spring permanent magnets. J. Appl. Phys. 2006, 99, 08B508. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Yue, M.; Liu, W.Q.; Chen, J.W.; Yi, X.F. Magnetic domain switching in Nd-Fe-B sintered magnets with superior magnetic properties. Mater. Res. Lett. 2018, 6, 255–260. [Google Scholar] [CrossRef]
- Nishino, M.; Uysal, I.E.; Hinokihara, T.; Miyashita, S. Dynamical aspects of magnetization reversal in the neodymium permanent magnet by a stochastic Landau-Lifshitz-Gilbert simulation at finite temperature: Real-time dynamics and quantitative estimation of coercive force. Phys. Rev. B 2020, 102, 020413. [Google Scholar] [CrossRef]
- Givord, D.; Li, H.S.; Moreau, J.M. Magnetic properties and crystal structure of Nd2Fe14B. Solid State Commun. 1984, 50, 497–499. [Google Scholar] [CrossRef]
- Iida, T.; Saito, T.; Shinagawa, K.; Tsushima, T. Field-induced spin reorientation in Nd2Fe14B and Er2Fe14B. J. Magn. Magn. Mater. 1992, 104, 1363–1364. [Google Scholar] [CrossRef]
- Mo, W.; Zhang, L.; Shan, A.; Cao, L.; Wu, J.; Komuro, M. Improvement of magnetic properties and corrosion resistance of NdFeB magnets by intergranular addition of MgO. J. Alloy. Compd. 2008, 461, 351–354. [Google Scholar] [CrossRef]
- Ramlan; Muljadi; Sardjono, P.; Gulo, F.; Setiabudidaya, D. Crystal structure and magnetic properties of Nd2Fe14B powder prepared by using high energy milling from elements metal Nd,Fe,B powders. J. Phys. Conf. Ser. 2016, 776, 012013. [Google Scholar] [CrossRef] [Green Version]
- Sagawa, M.; Fujimura, S.; Yamamoto, H.; Matsuura, Y.; Hirosawa, S. Magnetic properties of rare-earth-iron-boron permanent magnet materials. J. Appl. Phys. 1985, 57, 4094–4096. [Google Scholar] [CrossRef]
- Leliaert, J.; Dvornik, M.; Mulkers, J.; De Clercq, J.; Milošević, M.V.; Van Waeyenberge, B. Fast micromagnetic simulations on GPU—recent advances made with. J. Phys. D Appl. Phys. 2018, 51, 123002. [Google Scholar] [CrossRef]
- Vansteenkiste, A.; Leliaert, J.; Dvornik, M.; Helsen, M.; Garcia-Sanchez, F.; Van Waeyenberge, B. The design and verification of MuMax3. AIP Adv. 2014, 4, 107133. [Google Scholar] [CrossRef] [Green Version]
- Hahn, M.B. Temperature in micromagnetism: Cell size and scaling effects of the stochastic Landau–Lifshitz equation. J. Phys. Commun. 2019, 3, 075009. [Google Scholar] [CrossRef]
- Kirschner, M.; Schrefl, T.; Dorfbauer, F.; Hrkac, G.; Suess, D.; Fidler, J. Cell size corrections for nonzero-temperature micromagnetics. J. Appl. Phys. 2005, 97, 10E301. [Google Scholar] [CrossRef]
- Dickinson, R.; Royappa, A.T.; Tone, F.; Ujj, L.; Wu, G. Distribution of non-uniform demagnetization fields in paramagnetic bulk solids. J. Appl. Phys. 2011, 110, 013902. [Google Scholar] [CrossRef] [Green Version]
- Osborn, J.A. Demagnetizing Factors of the General Ellipsoid. Phys. Rev. 1945, 67, 351. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, N.; Han, H.-S.; Choi, C.-J.; Lee, K.-S.; Park, J. Calculation of Three-dimensional Energy Product for Isotropic Nd2Fe14B Magnet. Appl. Sci. 2022, 12, 7887. https://doi.org/10.3390/app12157887
Kim N, Han H-S, Choi C-J, Lee K-S, Park J. Calculation of Three-dimensional Energy Product for Isotropic Nd2Fe14B Magnet. Applied Sciences. 2022; 12(15):7887. https://doi.org/10.3390/app12157887
Chicago/Turabian StyleKim, Namkyu, Hee-Sung Han, Chul-Jin Choi, Ki-Suk Lee, and Jihoon Park. 2022. "Calculation of Three-dimensional Energy Product for Isotropic Nd2Fe14B Magnet" Applied Sciences 12, no. 15: 7887. https://doi.org/10.3390/app12157887