Contact of Rough Surfaces: An Incremental Model Accounting for Strain Gradient Plasticity

Abstract

In the contact of rough surfaces, most contact patches are at the scale of micrometers, and thus, their contact deformation can be dominated by the size-dependent plasticity. In this paper, we propose a new strategy to analyze the role of strain gradient plasticity in the contact response between a realistic rough surface and a rigid plane, which modifies the incremental contact model based on the mechanism-based gradient plasticity (MSGP) theory. For several different rough surfaces with their topography measured experimentally, the relations between applied load and real contact area are derived in a simple but effective way. It is found that strain gradient plasticity significantly increases the level of mean contact pressure. The hardening effect caused by strain gradient plasticity weakens somewhat as the contact area increases. Compared with previous methods, the present model might be more efficient and of wider application.

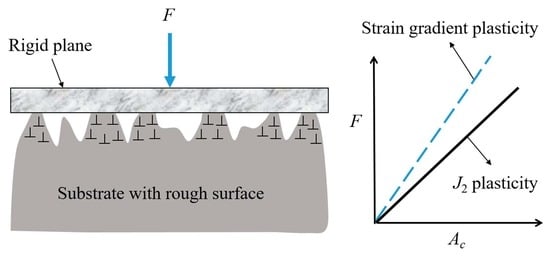
1. Introduction

The contact mechanics of rough solids play a fundamental role in many physical phenomena and engineering applications. Due to the inevitable roughness, it is now widely accepted that the real contact area between contacting bodies that is intimately related to friction, wear, sealing, and lubrication is generally a small fraction of the apparent one. However, to give an accurate prediction of the real contact area for a realistic rough surface is still challenging since the surface roughness is of great randomness and irregularity, and the contacting asperities usually involve complex deformation mechanisms.

Over the past few decades, theoretical investigation on the contact of rough surfaces has experienced a flourishing development [1,2,3]. The statistical multi-asperity contact models that originated from the pioneering work by Greenwood and Williamson (GW) [4] take a great proportion in this field, which ideally simplify the asperities on the rough surface by smooth spheres or paraboloids with randomly distributed heights and sizes. In the elementary multi-asperity models, the contacting asperities were assumed to deform elastically without interaction and obey the classical Hertz theory [4,5,6]. Such assumptions were later relaxed in the improved multi-asperity models. For example, Chang et al. [7] and, later, Kogut and Etsion [8] modified the GW model by considering the elastic-plastic deformation of asperities. The non-negligible interaction and coalescence between adjacent asperities were taken into account for large contact area fractions [9,10,11]. To obtain the relationship between real contact area and normal load in dry and lubricated contacts, the GW model was also extended to the contact of rough surfaces in the presence of foreign particles [12,13]. Apart from the multi-asperity models, fractal contact models were established that were based on the nature of self-affine rough surfaces [14,15]. With the concept of magnification and the power spectral density of roughness, Persson [16,17] proposed a scaling contact theory of rough surfaces. Using the profilometric model to calculate the contact area, Wang et al. [18] developed an incremental equivalent model to analyze the contact of elastic rough surfaces, which was later extended to the elastic-plastic cases [19,20]. Moreover, Hyun et al. [21] applied a finite element method to address the elastic contact of self-affine fractal surfaces. Boundary element-based approaches were also widely employed to calculate the contact responses between a rigid rough surface and an elastic substrate [22]. In the contact models mentioned above, the asperity deformation at all length scales was described by the classical elastic (plastic) theories, and the real contact area was found to be generally proportional to the applied normal load at small loads. Recently, it was suggested that accounting for some new scale-dependent mechanisms, such as strain gradient [23,24], adhesion [25], and surface effect [26], could be indispensable when analyzing the asperity deformation of rough surfaces, since the size of most asperities is on the order of microns or even down to sub-micrometers.

Size-dependent plasticity has been repeatedly demonstrated in the experiments of torsion [27], bending [28], and indentation [29,30,31] for crystalline materials at scales below tens of micrometers. Particularly, the indentation hardness was found to be larger if measured at a smaller indentation size [29,30,31]. Such an indentation size effect cannot be interpreted in the framework of classical plastic theory where the flow stress is determined only by the strain. Fleck et al. [27] pointed out that the size effect should be attributed to the geometrically necessary dislocations that result from the large strain gradient in a small material volume. Therefore, besides the homogeneous strain, the flow stress is also closely related to the strain gradient [27,32]. Based on the Taylor dislocation hardening model, Gao et al. [33] proposed the mechanism-based strain gradient plasticity theory (MSGP), which links the density of geometrically necessary dislocations to the effective strain gradient. With this MSGP theory, Huang et al. [34] performed a finite element analysis of the microindentation test, which successfully reproduced the experimental observed linear dependence of the square of indentation hardness on the inverse of indention depth. The MSGP theory was later modified into a low-order version without introducing high-order stress [35]. To study the effect of size-dependent plasticity on the contact performance of rough surfaces, Song et al. [23] and You et al. [24] built three-dimensional finite element models with this low-order theory of MSGP. Numerical results were presented to illustrate the significant role of strain gradient plasticity. Compared with the classical J₂ isotropic plasticity, strain gradient plasticity leads to a higher slope of the linear relationship between normal load and real contact area.

Considering the surface roughness and the micro-scale effect of plasticity, it is a cumbersome task to derive the real contact area between rough solids by implementing the finite element simulations through the user-defined subroutines of commercial finite element software. Alternatively, a simple but effective theoretical method would be more attractive in the parametric analysis of rough surface contact. Up to now, few works have been directed to achieve this goal. Recently, Song et al. [36] succeeded in extending the original GW model to incorporate size-dependent plasticity and asperity interaction. However, the underlying assumption in the GW-based model that surface asperities are modeled by smooth spheres with their heights following Gaussian distribution confines its applicability.

In the present paper, we employ the incremental contact model proposed by Wang et al. [18] to study the contact between a rigid plane and a deformable rough surface considering strain gradient plasticity. It is assumed that the contact of rough surfaces is equivalent to the accumulation of identical circular contacts with radii estimated from the total contact area and the number of contact patches, which are directly obtained from the truncation sections of the rough surface at different heights. Different from the GW-based models, the incremental contact model does not require the ideal rough surface description using smooth spherical or paraboloidal asperities and is not limited to the isotropic Gaussian surfaces and, thus, is of wider application range. Here, we consider realistic rough surfaces of copper, which were generated by rubbing with sandpaper and measured with a white light interferometer. The plasticity of the rough surfaces is handled based on the MSGP theory. The interaction between surfaces is assumed frictionless and non-adhesive.

In Section 2, we describe the fundamental principle of the incremental contact model of rough surfaces. In Section 3, the explicit expression of the circular flat contact stiffness is derived based on the finite element analysis using the MSGP theory, which is the key in the incremental contact model accounting for strain gradient plasticity. In Section 4, the effect of strain gradient plasticity on the relation between normal load and real contact area is presented. The main conclusions are summarized in Section 5.

2. The Incremental Contact Model

For the elastic contact between a rough surface and a rigid plane, Wang et al. [18] first developed an incremental equivalent circular model to establish the relationship between normal load and real contact area, provided the surface topography and material properties are known. This model was validated through a comparison of the predicted results with the corresponding finite element simulations [18,19,20]. In this work, we further extend this incremental model to the contact of rough surfaces by taking into account the size-dependent plasticity.

Figure 1a schematically depicts the contact problem that a deformable rough surface is compressed by a rigid plane under a normal load F. According to the incremental contact model [18], the resulting contact area can be equivalently represented by the geometrically truncated area of the original rough surface at the separation z. As shown in Figure 1b, the contact region A_c(z) consists of a series of separated contact patches. The number of contact patches is denoted by N(z). Then, these irregular contact patches are equivalently simplified by identical circular contact patches (Figure 1c) with the radius determined by

$$r\left(z\right)={\left[\frac{A_c\left(z\right)}{\pi N\left(z\right)}\right]}^{1/2}$$

(1)

For a decrement of surface separation dz, the corresponding increment of normal load dF can be obtained by the current contact stiffness of the rough surface. Neglecting the interaction between neighboring contact patches, the current contact stiffness can be expressed by [18]

$$\frac{\mathrm{d}F}{\mathrm{d}z}=N\left(z\right)k\left(r\right)$$

(2)

where k(r) is the contact stiffness of an individual circular patch with a radius of r.

For the linear elastic material with elastic modulus E and Poisson’s ratio ν, k(r) is given by 2E^*r [37], where E^* = E / (1 − ν²) is the combined elastic modulus. For the elastic-plastic materials, k(r) relies not only on the radius of the contact patch r but also on the mean contact pressure F/A_c(z) and the plastic material parameters [19,20]. In this work, the plastic contact deformation is considered based on the MSGP theory, and thus, k(r) also depends on the intrinsic material length for the strain gradient plasticity. Explicit expression of k(r) is presented in Section 3.

By using the fourth-order Runge–Kutta method, the differential equation Equation (2) can be numerically solved with the initial condition of F(z→∞) = 0. As a result, the normal load F can be obtained as a function of separation z. Meanwhile, the real contact area A_c is given by the truncated area at separation z. Based on A_c(z) and F(z), the load-area relation for the contact of rough surfaces can be established.

It should be pointed out that the contact area A_c(z) and the number of contact patches N(z) at different separation z are the requisites in this incremental contact model. For realistic rough surfaces, it is almost impossible to derive general analytical expressions of A_c(z) and N(z). As an option, they can be calculated by using a numerical technique as the surface topography is measured. More details about the computations of A_c(z) and N(z) can be referred to in the previous works [18,19].

3. Circular Flat Contact with Strain Gradient Plasticity

To obtain the normal contact stiffness of each circular contact patch, finite element simulations are implemented for the axisymmetric contact between an elastic-plastic substrate and a micro-sized circular flat punch. In the finite element formulation based on the principle of virtual work, the basic equations from the theory of MSGP are employed [33,34].

3.1. Material Constitutive Model of MSGP

Macroscopically, most ductile crystalline materials follow the typical strain hardening model with linear elasticity and power-law hardening plasticity. During plastic deformation, the flow stress σ_flow can be expressed as a function of the strain by

$${\sigma }_{\mathrm{flow}}={\sigma }_y{\left(\frac{\epsilon }{{\sigma }_y/E}\right)}^n$$

(3)

where σ_y is the initial yield stress in uniaxial tension, ε is the effective strain, and n is the plastic work hardening exponent.

From the microscopic perspective, the plastic hardening phenomenon of crystalline material is generally caused by the movement and stacking of statistically stored dislocations (SSD) and geometrically necessary dislocations (GND) [32,33]. Based on the Taylor dislocation model that is assumed valid in the theory of MSGP [32,33], the shear flow stress τ_flow can be written in terms of dislocation density as

$${\tau }_{\mathrm{flow}}=\alpha \mu b\sqrt{{\rho }_T}=\alpha \mu b\sqrt{{\rho }_S+{\rho }_G}$$

(4)

where α is an empirical coefficient, μ is the shear modulus, b is the magnitude of the Burgers vector, and ρ_T is the total dislocation density equaling the summation of SSD density ρ_S and GND density ρ_G.

With the shear flow stress, the tensile flow stress can be given by

$${\sigma }_{\mathrm{flow}}=M{\tau }_{\mathrm{flow}}=M\alpha \mu b\sqrt{{\rho }_S+{\rho }_G}$$

(5)

where M is the Taylor factor.

In the framework of isotropic plasticity, the density of GND ρ_G is related to the effective plastic strain gradient η by [38,39]

$${\rho }_G=\frac{\lambda \eta }{b}$$

(6)

where λ is the Nye factor [40].

In addition, the density of SSD ρ_S can be determined by combining Equations (3) and (5) in the absence of the strain gradient (η = 0), that is

$${\rho }_S={\left(\frac{{\sigma }_{\mathrm{ref}}}{M\alpha \mu b}\right)}^2{\epsilon }^{2n}$$

(7)

where σ_ref is the reference stress in uniaxial tension given by

$${\sigma }_{\mathrm{ref}}=\frac{{\sigma }_y}{{\left({\sigma }_y/E\right)}^n}$$

(8)

Substituting Equations (6) and (7) into Equation (5) gives the flow stress as

$${\sigma }_{\mathrm{flow}}={\sigma }_{\mathrm{ref}}\sqrt{{\epsilon }^{2n}+l\eta }$$

(9)

It can be observed that the flow stress consists of two hardening contributions: the strain hardening ε²ⁿ and the strain gradient plasticity hardening lη. Here, l is the intrinsic material length of the strain gradient plasticity given by

$$l=M^2{\alpha }^{2}b\lambda {\left(\frac{\mu }{{\sigma }_{\mathrm{ref}}}\right)}^2$$

(10)

For the face-centered-cubic (fcc) polycrystalline materials, the Taylor factor M is equal to 3.06, and the Nye factor λ is on the order of 2 [34]. Therefore, the intrinsic material length can be approximately written as

$$l=18{\alpha }^{2}b{\left(\frac{\mu }{{\sigma }_{\mathrm{ref}}}\right)}^2$$

(11)

which is typically on the order of micrometers.

According to Equation (9), it can be understood that a higher strain gradient results in a higher flow stress under the same amount of strain, corresponding to the experimental observation that the sample has a higher indentation hardness measured at a smaller depth [29,30,31]. With the microscopic plasticity law accounting for strain gradient, the constitutive equations in the deformation theory of MSGP are given as [33,34]

$$\begin{array}{l}{\sigma }_{ij}=K{\epsilon }_{kk}{\delta }_{ij}+\frac{2{\sigma }_{\mathrm{flow}}}{3\epsilon }{{\epsilon }^{\prime }}_{ij}\\ {\tau }_{ijk}=l_{\epsilon }{}^2\left[\frac{K{\eta }_{ijk}^{\mathrm{H}}}{6}+\frac{{\sigma }_{\mathrm{flow}}}{\epsilon }\left({{\Lambda }}_{ijk}-{{\Pi }}_{ijk}\right)+\frac{{\sigma }_{\mathrm{ref}}{}^2}{{\sigma }_{\mathrm{flow}}}n{\epsilon }^{2n-1}{{\Pi }}_{ijk}\right]\end{array}$$

(12)

where σ_ij is the Cauchy stress tensor, ε_ij is the strain tensor, K is the elastic bulk modulus, ε′_ij represents the deviatoric strain defined by ε′_ij = ε_ij − ε_kkδ_ij/3 (thus, the effective strain can be determined by ε = (2ε′_ijε′_ij/3)^1/2), the flow stress σ_flow is given by Equation (9), τ_ijk is the high order stress tensor, η_ijk is the strain gradient tensor, ${\eta }_{ijk}^{\mathrm{H}}$ represents the volumetric part of the strain gradient tensor defined by ${\eta }_{ijk}^{\mathrm{H}}$ = (η_jppδ_ik + η_ippδ_jk)/4, the effective strain gradient η is related to the deviatoric strain gradient η′_ijk (defined by η′_ijk = η_ijk – ${\eta }_{ijk}^{\mathrm{H}}$) by η = (η′_ijkη′_ijk)^1/2/2), l_ε is the mesoscale cell size given by l_ε = 5bμ/σ_y, and Λ_ijk and Π_ijk are given by

$$\begin{array}{l}{{\Lambda }}_{ijk}=\frac{1}{72}\left(2{{\eta }^{\prime }}_{ijk}+{{\eta }^{\prime }}_{kji}+{{\eta }^{\prime }}_{kij}+\frac{1}{2}{\eta }_{kpp}{\delta }_{ij}+\frac{1}{3}{\eta }_{ijk}^{\mathrm{H}}\right)\\ {{\Pi }}_{ijk}=\frac{1}{54{\epsilon }^2}\left[{{\epsilon }^{\prime }}_{mm}\left({{\epsilon }^{\prime }}_{ik}{{\eta }^{\prime }}_{jmn}+{{\epsilon }^{\prime }}_{jk}{{\eta }^{\prime }}_{imn}\right)+\frac{1}{4}{\eta }_{qpp}\left({{\epsilon }^{\prime }}_{ik}{{\epsilon }^{\prime }}_{jq}+{{\epsilon }^{\prime }}_{jk}{{\epsilon }^{\prime }}_{iq}\right)\right]\end{array}$$

(13)

respectively.

3.2. Finite Element Analysis

In the contact simulations accounting for strain gradient plasticity, the isoparametric element developed by Wei and Hutchinson [41] is adopted. It was shown that this type of element worked well in the finite element analysis of microindentation experiments [34]. For the considered contact problem, choosing this type of element should bring about reasonable results.

Through the user-defined element subroutine in the commercial finite element software ABAQUS, the nine-node axisymmetric quadrilateral isoparametric elements are defined to discretize the substrate. As shown in Figure 2, the mesh near the contact region is highly refined, whereas relatively coarse mesh is used for the part far from the indenter. The size of the smallest element is approximately 0.05 μm, which is much smaller than the global size of the substrate. The accuracy of the simulation results has been ensured through mesh convergence tests, which found that a mesh with approximately 33,000 elements is sufficient for our simulations. The flat punch with a radius of r is set as the analytic rigid. To reduce the stress concentration at the edge of the punch, a tiny fillet with a radius of 0.01r is introduced, which has a negligible effect on the overall contact response. Note that the contact interface is assumed as non-adhesive and frictionless. The bottom of the substrate is constrained in the direction of the z-axis, while the radial displacement is restricted at the axis of symmetry.

The substrate is modelled by a homogeneous and isotropic solid of polycrystalline copper. With the standard uniaxial tensile tests on a servo-hydraulic testing machine (MTS-858/2.5T, MTS), the material parameters of the copper were measured in [42]: elastic modulus E = 105.6 GPa, Poisson’s ratio ν = 0.34, yield stress σ_y = 159.6 MPa, and hardening exponent n = 0.13. For the copper, the magnitude of Burgers vector is b = 0.255 nm [34]. By varying the empirical coefficient α in the Taylor model, a series of values of l can be assumed by Equation (10).

3.3. Explicit Expression of Contact Stiffness

Based on the dimensional analysis and the results in [19], the relationship between contact load P and indentation depth δ can be described by

$$\frac{P}{\pi r^2{\sigma }_y}=f\left(\frac{2E^{*}\delta }{\pi {\sigma }_{y}r},\frac{l}{r}\right)$$

(14)

where the ratio l/r determines the effect of strain gradient plasticity.

With the finite element simulations, the contact load can be obtained as a function of indentation depth for the circular flat contacts with different l and r. Figure 3 displays the variation of the normalized load P/(πr²σ_y) with respect to the normalized depth 2E^*δ/(πσ_yr) for l/r = 0, 1.07, 9.65, 34.3, and 68.6. In the elastic regime of P/(πr²) < σ_y, the load increases linearly with depth following the classical elastic contact solution, i.e., P = 2E^*rδ [37]. With an accumulation of plastic deformation, the load-depth relation gradually diverges from the linearity and essentially becomes dependent on the strain gradient plasticity parameter l/r. When the contact radius is much larger than the intrinsic material length, i.e., l/r → 0, our results agree well with the prediction of Ding et al. [20] using J₂ plasticity. For the contact with a larger l/r, a higher load is required to generate the same depth, which implies a stronger hardening effect due to strain gradient plasticity. It should be pointed out that the finite simulations were performed for a large number of contact cases. For the sake of clarity, only several results are displayed.

Based on the curve fitting of the numerical results, it was found that the dimensionless function in Equation (14) can be expressed in the form of

$$f\left(\frac{2E^{*}\delta }{\pi {\sigma }_{y}r},\frac{l}{r}\right)=\frac{2E^{*}\delta }{\pi {\sigma }_{y}r}{\left[1+a_l{\left(\frac{2E^{*}\delta }{\pi {\sigma }_{y}r}\right)}^{b_l}\right]}^{c_l}$$

(15)

where a_l, b_l, and c_l are fitting coefficients that depend only on the ratio of the intrinsic material length l to the radius of contact r.

For the circular contact between a rigid flat punch and a substrate, the contact stiffness k(r) is defined by the derivative of contact load P with respect to indentation depth δ. In view of Equation (14), the contact stiffness k(r) normalized by 2E^*r can be expressed in terms of the strain gradient plasticity parameter l/r and the mean contact pressure P/(πr²) normalized by the yield stress σ_y,

$$\frac{k\left(r\right)}{2E^{*}r}=g\left(\frac{l}{r},\frac{P}{\pi r^2{\sigma }_y}\right)$$

(16)

For a given strain gradient plasticity parameter l/r, the variation of the normalized contact stiffness with respect to the normalized mean contact pressure can be determined from Equations (14) and (15). To avoid implicit expression, the dimensionless function in Equation (16) is expressed in an explicit form as

$$g\left(\frac{l}{r},\frac{P}{\pi r^2{\sigma }_y}\right)={\left[1+m_l{\left(\frac{P}{\pi r^2{\sigma }_y}\right)}^{2.2}\right]}^{n_l}$$

(17)

where m_l and n_l are fitting coefficients.

For a series of l/r, the corresponding fitting coefficients of m_l and n_l can be obtained by curve fitting, and it is found that the dependences of m_l and n_l on the ratio l/r ranging from 0 to 2 can be further fitted by

$$\begin{array}{l}{m}_l=\frac{0.25{\left(l/r\right)}^2+0.022\left(l/r\right)+0.011}{{\left(l/r\right)}^3+0.27{\left(l/r\right)}^2+0.52\left(l/r\right)+0.22}\\ n_l=-\frac{6.32{\left(l/r\right)}^2+2.69\left(l/r\right)+1.17}{{\left(l/r\right)}^3+8.06{\left(l/r\right)}^2+0.72\left(l/r\right)+0.34}\end{array}$$

(18)

For the contact of a rough surface with a rigid plane, we can derive its relationship between real contact area and normal load based on the incremental contact model as described in Section 2, where strain gradient plasticity is accounted for with the contact stiffness k(r) given by Equation (16).

4. Results and Discussion

Figure 4 shows the topographies of three different realistic copper rough surfaces (S1, S2, and S3), which were generated by rubbing with sandpaper and measured with a white light interferometer over a nominal area of approximately 1 mm². The dependences of contact area A_c(z) and contact patch number N(z) on the separation z were given in [42]. The mean radii of the contact patches of these surfaces are calculated by Equation (1) with A_c(z) and N(z). As shown in Figure 5, the mean radii of the contact patches are on the order of micrometers for small contact areas. Thus, it is expected that the effect of strain gradient plasticity should be considerable in the contact of these rough surfaces.

Figure 6, Figure 7 and Figure 8 show the area-load relation for surfaces S1, S2, and S3, respectively, with different intrinsic material length l. For the cases with small intrinsic material length, our results approach the prediction based on the classical J₂ plasticity [20]. When the strain gradient plasticity is taken into account, it is found that the area-load relation is still as close to linear at small loads as that obtained based on the classical plastic theory. However, the slope that represents the mean pressure over the real contact area increases significantly with the intrinsic material length. Such a hardening trend is qualitatively consistent with the finite element results of Song et al. [23]. It is worth mentioning that Yuan et al. [26] analyzed the contact of rough surfaces with surface effect and also found the proportionality between load and area was raised, which is a mechanism at nanoscale that is different from the present strain gradient plasticity at the scale of micrometers.

To characterize the hardening degree of the rough surface contact considering strain gradient plasticity, we introduce a dimensionless factor as

$$\theta =\frac{F_{\mathrm{MSGP}}-F_{J2}}{F_{J2}}\times 100\%$$

(19)

where F_MSGP and F_J2 represent the normal loads obtained based on the MSGP theory and the classical theory of J₂ plasticity, respectively.

Figure 9, Figure 10 and Figure 11 display the variation of the hardening factor θ with respect to the contact area A_c for surfaces S1, S2, and S3, respectively. Overall, the hardening factor gets smaller with increasing contact area, which is basically caused by the expanding of the contact patches. For the considered rough surfaces, it can be observed from Figure 5 that the mean radius of the contact patches for the contact area of 0.2 mm² (approximately 20% of the nominal area) is approximately triple that for the contact area of 0.01 mm² (approximately 1% of the nominal area). Correspondingly, the hardening factor for l = 10 μm is found to decrease by approximately one third as the contact area increases from 1% to 20% of the nominal area. The hardening effect of strain gradient plasticity in the contact of rough surfaces is particularly sensitive and prominent for initial contact where the size of the contact patches is relatively small.

It should be pointed out that the contact analysis of rough surfaces accounting for strain gradient plasticity was addressed earlier by Song et al. [23,36] with both direct finite element simulations and a modified multi-asperity GW model. Compared with their approaches, our model is more straightforward and convenient. With the present model, the real contact area generated by a given normal load can be handily predicted once the surface topography and the material parameters are measured. This advantage could be meaningful in the design and mechanical fabrication of solid surfaces as well as in the study of tribological problems, such as friction, sealing, wear, and lubrication.

The present contact model does not take into account both the elastic and plastic interactions between contact patches. For large contact area fractions, such interactions would be non-negligible as the stresses between the contact patches could be significantly high, and the present model should be further modified. In addition, the material of the rough surface, for simplicity, is assumed isotropic and homogeneous without any defects. The effects of local inhomogeneity and defects in the contacting asperities on the contact response is beyond the scope of the present work and deserves future investigations.

5. Concluding Remarks

The incremental contact model for rough surfaces is extended to account for strain gradient plasticity based on the MSGP theory. Through finite element analysis, the contact stiffness of a single circular flat punch is presented in an explicit form, which is higher as the ratio of intrinsic material length to contact radius increases. For three different realistic rough surfaces, the area-load relations are derived by employing the modified incremental contact model. Strain gradient plasticity does not change the linear nature of the area-load relation but increases the slope, which is the mean contact pressure. This trend is qualitatively consistent with the results in the literature. In addition, for the considered rough surfaces, the hardening degree of strain gradient plasticity could decrease by approximately one third as the contact area increases from approximately 1% to 20% of the nominal area. This work provides a simple but efficient approach to predict the real contact area under a given load for a rough surface considering strain gradient plasticity. On the basis of the present model, more advanced analysis can be conducted by considering other factors, such as asperity interactions and material inhomogeneity.