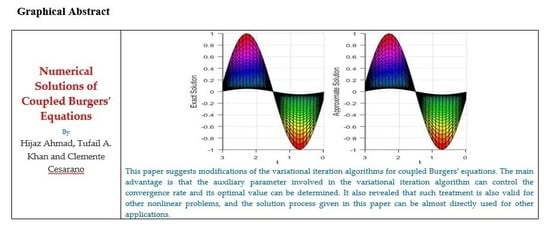
Numerical Solutions of Coupled Burgers’ Equations
Abstract
:1. Introduction
2. Modified Variational Iteration Algorithm-II
3. Numerical Assessments
3.1. Test Problem 1
3.2. Test Problem 2
3.3. Test Problem 3
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Rashid, A.; Ismail, A.I.B.M. A Fourier Pseudospectral Method for Solving Coupled Viscous Burgers Equations. Comput. Methods Appl. Math. 2009, 9, 412–420. [Google Scholar] [CrossRef]
- Islam, S.-U.; Haq, S.; Uddin, M. A meshfree interpolation method for the numerical solution of the coupled nonlinear partial differential equations. Eng. Anal. Bound. Elem. 2009, 33, 399–409. [Google Scholar] [CrossRef]
- Khater, A.; Temsah, R.; Hassan, M. A Chebyshev spectral collocation method for solving Burgers’-type equations. J. Comput. Appl. Math. 2008, 222, 333–350. [Google Scholar] [CrossRef]
- Kaya, D. An explicit solution of coupled viscous Burgers′ equation by the decomposition method. Int. J. Math. Math. Sci. 2001, 27, 675–680. [Google Scholar] [CrossRef]
- Mittal, R.; Arora, G. Numerical solution of the coupled viscous Burgers’ equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1304–1313. [Google Scholar] [CrossRef]
- Lai, H.; Ma, C. A new lattice Boltzmann model for solving the coupled viscous Burgers’ equation. Phys. A: Stat. Mech. Appl. 2014, 395, 445–457. [Google Scholar] [CrossRef]
- Rashid, A.; Abbas, M.; Ismail, A.I.M.; Majid, A.A. Numerical solution of the coupled viscous Burgers equations by Chebyshev–Legendre Pseudo-Spectral method. Appl. Math. Comput. 2014, 245, 372–381. [Google Scholar] [CrossRef]
- Kumar, M.; Pandit, S. A composite numerical scheme for the numerical simulation of coupled Burgers’ equation. Comput. Phys. Commun. 2014, 185, 809–817. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mokhtari, R. A reproducing kernel method for solving a class of nonlinear systems of pdes. Math. Model. Anal. 2014, 19, 180–198. [Google Scholar] [CrossRef]
- Bak, S.; Kim, P.; Kim, D. A semi-Lagrangian approach for numerical simulation of coupled Burgers’ equations. Commun. Nonlinear Sci. Numer. Simul. 2019, 69, 31–44. [Google Scholar] [CrossRef]
- Inokuti, M.; Sekine, H.; Mura, T. General Use of the Lagrange Multiplier in Nonlinear Mathematical Physics; Pergamon Press: Oxford, UK, 1978. [Google Scholar]
- He, J.-H.; Wu, G.-C.; Austin, F. The variational iteration method which should be followed. Nonlinear Sci. Lett. A 2010, 1, 1–30. [Google Scholar]
- Ahmad, H. Variational Iteration Algorithm-I with an Auxiliary Parameter for Solving Fokker-Planck Equation. Earthline J. Math. Sci. 2019, 2, 29–37. [Google Scholar] [CrossRef]
- Ahmad, H.; Khan, T.A. Variational iteration algorithm-I with an auxiliary parameter for wave-like vibration equations. J. Low Freq. Noise Vib. Act. Control 2019, 38, 1113–1124. [Google Scholar] [CrossRef] [Green Version]
- Anjum, N.; He, J.-H. Laplace transform: Making the variational iteration method easier. Appl. Math. Lett. 2019, 92, 134–138. [Google Scholar] [CrossRef]
- Yu, D.-N.; He, J.-H.; Garcıa, A.G. Homotopy perturbation method with an auxiliary parameter for nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control 2018, 38, 1540–1554. [Google Scholar] [CrossRef]
- He, J.-H. Variational approach to the Thomas–Fermi equation. Appl. Math. Comput. 2003, 143, 533–535. [Google Scholar] [CrossRef]
- He, J.-H. Variational iteration method—Some recent results and new interpretations. J. Comput. Appl. Math. 2007, 207, 3–17. [Google Scholar] [CrossRef]
- He, J.-H.; Wu, X.-H. Variational iteration method: New development and applications. Comput. Math. Appl. 2007, 54, 881–894. [Google Scholar] [CrossRef] [Green Version]
- Nadeem, M.; Ahmad, H. Variational Iteration Method for Analytical Solution of the Lane-Emden Type Equation with Singular Initial and Boundary Conditions. Earthline J. Math. Sci. 2019, 127–142. [Google Scholar] [CrossRef]
- Ahmad, H. Variational iteration method with an auxiliary parameter for solving differential equations of the fifth order. Nonlinear Sci. Lett. A 2018, 9, 27–35. [Google Scholar]
- Rafiq, M.; Ahmad, H.; Mohyud-Din, S.T. Variational iteration method with an auxiliary parameter for solving Volterra’s population model. Nonlinear Sci. Lett. A 2017, 8, 389–396. [Google Scholar]
- Nadeem, M.; Li, F.; Ahmad, H. Modified Laplace variational iteration method for solving fourth-order parabolic partial differential equation with variable coefficients. Comput. Math. Appl. 2019, 78, 2052–2062. [Google Scholar] [CrossRef]
- He, J.-H. Lagrange crisis and generalized variational principle for 3D unsteady flow. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- He, J.-H.; Sun, C. A variational principle for a thin film equation. J. Math. Chem. 2019, 57, 2075–2081. [Google Scholar] [CrossRef]








| CBCS [5] | LBM [6] | CBSLM [10] | MVIA-II | MVIA-I | CBCS [5] | LBM [6] | CBSLM [10] | MVIA-II | MVIA-I | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.1 | 0.3 | 6.7307 | 6.7736 | 5.7744 | 7.0326 | 2.2440 | 6.5947 | 6.6014 | 5.6194 | 6.7509 | 2.1840 |
| 1.0 | 0.1 | 0.3 | 1.3173 | 1.3317 | 0.2346 | 1.4073 | 4.4886 | 1.3020 | 1.3045 | 1.2083 | 1.3500 | 4.3681 |
| 5.0 | 0.1 | 0.3 | 5.9329 | 6.1433 | 6.0584 | 7.0707 | 2.2464 | 6.1046 | 6.1515 | 6.0644 | 6.7445 | 2.1844 |
| 10 | 0.1 | 0.3 | 1.0760 | 1.1439 | 1.1365 | 1.4221 | 4.4981 | 1.1541 | 1.1713 | 1.1633 | 1.3468 | 4.3694 |
| CBCS [5] | LBM [6] | CBSLM [10] | MVIA-II | MVIA-I | CBCS [5] | LBM [6] | CBSLM [10] | MVIA-II | MVIA-I | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.1 | 0.3 | 5.0960 | 5.0505 | 4.3123 | 5.1860 | 2.5955 | 9.1286 | 5.6806 | 4.8567 | 6.2517 | 2.5169 | |
| 1.0 | 0.1 | 0.3 | 9.9228 | 9.8477 | 9.1399 | 1.0389 | 5.1920 | 1.8244 | 1.0942 | 1.0169 | 1.2509 | 5.0343 | |
| 5.0 | 0.1 | 0.3 | 4.3800 | 4.3984 | 4.3400 | 5.2635 | 2.5996 | 9.0708 | 4.6640 | 4.6046 | 6.2794 | 2.5190 | |
| 10 | 0.1 | 0.3 | 7.8592 | 8.0429 | 7.9933 | 7.8956 | 5.2084 | 1.0815 | 8.2714 | 8.2233 | 7.9438 | 5.0426 | |
| [9] | [3] | [5] | [1] | [2] | MVIA-II | MVIA-I | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 0.1 | 0.3 | 4:251 | 4:38 | 4:167 | 9:619 | 4:084 | 2.2743 | 1.1511 | |
| 1.0 | 0.1 | 0.3 | 8:150 | 8:66 | 8:258 | 1:153 | 8:157 | 4.5485 | 2.3024 | |
| 0.5 | 0.1 | 0.3 | 4:051 | 4:99 | 1:480 | 3:332 | 3:713 | 2.1639 | 6.9734 | |
| 1.0 | 0.1 | 0.3 | 7:158 | 9:92 | 4:770 | 1:162 | 7:358 | 4.3275 | 1.3949 |
| FDM [6] | LBM [6] | MVIA-II | FDM [6] | LBM [6] | MVIA-II | |
|---|---|---|---|---|---|---|
| 1.0 | 1.5724 | 1.4829 | 7.8577 | 6.2856 | 5.7788 | 6.1316 |
| 2.0 | 2.9383 | 2.7955 | 2.6625 | 1.1138 | 1.0754 | 1.5700 |
| 3.0 | 4.1676 | 3.9298 | 8.7801 | 1.5879 | 1.4861 | 5.1132 |
| 4.0 | 5.2504 | 4.9434 | 2.9783 | 1.9868 | 1.8800 | 1.6959 |
| 5.0 | 6.1878 | 5.8615 | 3.4271 | 2.3468 | 2.2034 | 1.8436 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, H.; Khan, T.A.; Cesarano, C. Numerical Solutions of Coupled Burgers’ Equations. Axioms 2019, 8, 119. https://doi.org/10.3390/axioms8040119
Ahmad H, Khan TA, Cesarano C. Numerical Solutions of Coupled Burgers’ Equations. Axioms. 2019; 8(4):119. https://doi.org/10.3390/axioms8040119
Chicago/Turabian StyleAhmad, Hijaz, Tufail A. Khan, and Clemente Cesarano. 2019. "Numerical Solutions of Coupled Burgers’ Equations" Axioms 8, no. 4: 119. https://doi.org/10.3390/axioms8040119