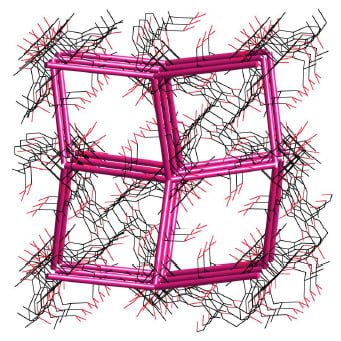
Let’s Talk about MOFs—Topology and Terminology of Metal-Organic Frameworks and Why We Need Them

Abstract

Recent IUPAC (The International Union for Pure and Applied Chemistry) recommendations on the terminology of metal-organic frameworks are reviewed and the background to a proposed topology classification is discussed. The various numerical designators such as point symbols, vertex symbols and transitivity are also explained and their importance elucidated.

1. Introduction

Terminology, and especially nomenclature, is sometimes frowned upon and regarded as hurdles rather helpers, probably because one needs to follow rules; perhaps not the practicing academic scientist’s best discipline.

While ill conceived and unnecessarily restrictive rules may indeed be hurdles, well-formulated nomenclature and terminology, thought trough with a view to the past, carful considerations of the present, and a clairvoyant eye on the future, are indeed of immense value both to scientific and economic development. One could for example note that IUPAC, the International Union for Pure and Applied Chemistry, was founded in 1919 just because international trade and immaterial rights needed a consistent and international vocabulary [1], and today cross border legislation such as the European Union’s REACH (Registration, Evaluation, Authorisation and Restriction of Chemicals) is another prime example of this need.

It stands to reason that a field with such wide reaching aspirations for its practical applications as Metal-Organic Frameworks, or its more specialized subgroup Porous Coordination Polymers, need to have an adequate nomenclature and terminology [2,3].

2. Terminology—General Classification

Terminology deals with all technical vocabulary excluding names of individual compounds. We will first discuss the name of the class of compounds colloquially known as “MOFs” (pronounced moffs) then go on to deal with more detailed descriptions of different MOFs in the next section.

2.1. Controversy of Metal-Organic Framework versus Coordination Polymer

This controversy can approximately be described as arising from different groups having different preconceptions of chemical bonding, specifically scientist with a solid state background, perhaps in zeolites, versus chemist predominantly practicing coordination chemistry. The more or less amicable arguments between the groups have been described and analyzed elsewhere [2,4], and did not reach the same magnitude as for example the controversy regarding gallium-gallium triple bonds in the late 1990s [5]. A consensus of an IUPAC expert group assembled in 2009 was given in the 2013 IUPAC recommendations on Terminology of Metal-Organic Frameworks and Coordination Polymers [6].

2.2. Definitions in the IUPAC 2013 Recommendations

We reiterate here the main recommendations [6]:

Definition of Coordination Polymer: “A coordination compound with repeating coordination entities extending in 1, 2 or 3 dimensions.”

Definition of Coordination Network: “A coordination compound extending, through repeating coordination entities, in 1 dimension, but with cross-links between two or more individual chains, loops or spiro-links, or a coordination compound extending through repeating coordination entities in 2 or 3 dimensions.”

Definition of Metal-Organic Framework: “A Metal-Organic Framework, abbreviated to MOF, is a Coordination Network with organic ligands containing potential voids.”

3. The IUPAC 2013 Recommendations Concerning Nets and Network Topologies

We first note that: “The use of topology and topology descriptors to enhance the description of crystal structures of MOFs and 3D-coordination polymers is strongly recommended” [6]. We then need to discuss briefly what topology and topology descriptors are and what makes them so essential in the MOF area that IUPAC strongly recommends their use.

3.1. Topology

A topology is invariant to bending, stretching and squeezing, but not to bond breaking and the concept of network topology is thus perfectly adapted to describe MOFs [7] as well as a number of other types of crystalline systems [8,9,10]. Network topology can in fact be regarded as a natural extension of the concept of stereoisomers such as E, Z, cis, trans, fac, and mer for molecular compounds and used in the same natural way. The suggested procedure for network topologies is to use the three letter codes from the Reticular Chemistry Structure Resource, RCSR, which we here will print in small letters and bold.

As soon as we get into particulates in organic chemistry we need to specify if an alkene is E or Z, and it should be self evident that we in the same way need to know if a 4-connected network has the diamond (dia), quartz (qtz) or any other topology, see Figure 1.

Figure 1. Network topologies with four-connected branching points or vertices: (a) The dia-net based on the diamond structure; (b) The chiral qtz-net based on the quartz structure; (c) The 2D sql-net.

Figure 1. Network topologies with four-connected branching points or vertices: (a) The dia-net based on the diamond structure; (b) The chiral qtz-net based on the quartz structure; (c) The 2D sql-net.

Every different network topology thus has its own arrangement of bonds and there exist of course an infinite number of such networks. Luckily though, only a handful of these occur with any regularity and you would normally find your network in the RCSR which list all the most common topologies and where you can download or copy the crystallographic parameters for each net [11,12,13].

For all but the most common, such as the dia-net or the six-connected net based on primitive cubic packing, the pcu-net in for example MOF-5, it is recommended to use freely available software. Two of these systems are continually updated, SYSTRE [14] that will give you the topology once you have decided about vertices and connectivity from your structure, and TOPOS [15,16] that have the possibility of a custom or a fully automated determination of the network topology as well as a complete structure analysis module.

There are many reasons to use network analysis besides that the firm IUPAC recommendations have been communicated to journal editors throughout the world. These have been elaborated elsewhere [9], but the four main selling points are:

(1)

Understand the structure of the materials you have prepared;

(2)

Compare your results to materials others have made;

(3)

Make your scientific communication more efficient;

(4)

Truly make something new by design.

Under point four we may also add that once you have made your design the topology can in fact help you solving the crystal structure if you need to rely on powder diffraction data [17].

Basically this is all you need to know, but it is good to have some idea of how we differentiate between the topologies, so I will here give you a brief idea of what these software packages do.

3.2. Topology Descriptors: The Point Symbol

The descriptor we can most easily inspect is the ring [18] size. We can count how many nodes in the network it takes to bring us back to our starting point via the shortest route. Just by inspection it is easy to discover four-rings, but already to differentiate between seven- and eight-rings becomes somewhat less obvious.

However, this is but a crude way and will give the same result for the dia and the qtz net in Figure 1, they both have six-rings as the shortest ring. So then we can make the concept a bit more detailed and instead count all the shortest rings emanating from a vertex via the different links that it has, giving us three numbers for a three-connected vertex, six for a four-connected vertex and so on. This is a more useful code called the point symbol [19], and is written with the ring sizes in ascending order with the number of rings in superscript.

Using this concept we can now differentiate between the dia- and the qtz-net as the former has point symbol 6⁶ and the latter point symbol 6⁴8².

3.3. Topology Descriptors: The Vertex Symbol

Sometime this will no be enough, for example the most symmetric of the three-connected nets, the chiral srs-net, and the non-chiral ths-net both have the point symbol 10³. We can then extend the concept and for each pair of links sticking out from a vertex calculate how many different ways we can construct these shortest rings. For a diamond net there are for example two different six-rings connecting each pair of links. This we call the vertex symbol [19], and we write this with subscripts for the number of possibilities and with multiplication dots in between each symbol. For srs we get 10₅·10₅·10₅ and for ths 10₂·10₄·10₄.

3.4. Topology Descriptors: The Coordination Sequence

There exists a very rare allotrope of carbon called lonsdaleite, a diamond twin that is hexagonal rather than cubic. Although it existence has recently been questioned [20], the corresponding lon-net is very real and has identical point and vertex symbols as the dia-net, 6⁶ and 6₂·6₂·6₂ 6₂ 6₂ 6₂ respectively, so how can we differentiate between them? The structural difference is that some of the six-rings are in boat rather than chair conformation, so that for clear cut cases, where the network of your structure is close to the ideal (most symmetric) form of one of the two nets they are quite easy to distinguish. But we need something we can compute and so turn to the coordination sequence which simply means that we grow the network from one point to its nearest neighbors and count how many these are. For the first point in a four-connected net these are obviously four, but for subsequent growth generations it gets complicated. Usually one computes these up to the 10th generation, sum up including generation 0, and report this as the td10 value. For the dia- and lon-nets this gives:

dia: 1 + 4 + 12 + 24 + 42 + 64 + 92 + 124 + 162 + 204 + 252 = 981

lon: 1 + 4 + 12 + 25 + 44 + 67 + 96 + 130 + 170 + 214 + 264 = 1027

In this way it is possible to computationally differentiate between the two, and most other nets that have identical point symbols. Topologies that have the same point symbol, vertex symbol and where the coordination sequence sums up to the same value in the 10th generation are in fact very rare, the pair of three- and six-connected nets edq and cdj being one such exception [21].

4. A Measure of Complexity: Transitivity and Genus

We now move to a different but useful concept, which is the transitivity of a net [21,22]. If we use nets as blueprints for MOFs then it would be good to have a measure, other than statistics from known structures, of how complex a network is. This because nature seem to have a strong preference for high symmetry solutions and simplicity, and if we specifically want to make something it is good to know exactly how complex the net is, so that we perhaps can take account for this in our synthetic strategy and not just mix, stir, and hope.

The pqrs Numbers, the Transitivity Symbol

There are two natural ways to describe the complexity of a net, the number of symmetry independent vertices and the number of different links between them, the lower these numbers the simpler the net. On the more abstract side there is the topology descriptor called genus that, with an oversimplification, can be related to the number of holes in a 3D body (a sphere or ellipsoid has g = 0, a torus g = 1, the dia-net g = 3).

In between these levels of abstraction we have a set of numbers, pqrs, called the transitivity of the net. This approach is based on nets as tilings and was suggested by O. Delgado-Friedrich et al. in 1999 and elaborated by O. Delgado-Friedrich M. O’Keeffe and O. M. Yaghi in subsequent years [23,24,25,26].

The transitivity is based on using the shortest rings in the net to construct polyhedra (the 3D-tiles) that completely fills space. If we do this, four parameters emerge that describe the tiling, the number of vertices (p); the number of edges or links (q); the number of faces (r); and the number of tiles (s), see Figure 2. This set of numbers now describes the complexity of the net, and they are independent of the type of connectivity at each node and the size of the rings formed.

Figure 2. (a) Fragment of the diamond net (dia). Different tiles marked in red, purple and blue. (b) Framework of two tiles; (c) Framework of two tiles separated; (d) Two tiles separated. This net has only one type of vertex (p), one type of edge (q) one type of face (r) and one type of tile (s), so it has the transitivity 1111.

Figure 2. (a) Fragment of the diamond net (dia). Different tiles marked in red, purple and blue. (b) Framework of two tiles; (c) Framework of two tiles separated; (d) Two tiles separated. This net has only one type of vertex (p), one type of edge (q) one type of face (r) and one type of tile (s), so it has the transitivity 1111.

It has been shown that there are only five nets with transitivity 1111, called the regular nets [25], these are the 3-connected srs-net, the 4-connected nbo- and dia-nets, the 6-connected pcu-net, and the 8-connected bcu-net. These five are in some sense the extended network analogues of the platonic bodies, the five polyhedra built from one kind of face and one kind of vertex.

It has been proposed to name other different classes of 3D-nets in descending order of symmetry in the following way [25,26]: quasiregular nets having the transitivity 1112 (there appear to be only one of these, fcu) and semiregular nets having the transitivity 11rs.

5. The Space within, Dual Nets and Interpenetration

5.1. Dual Nets

MOFs are often of interest because of the space inside them, and this can also be classified in terms of topology. To describe this potentially void space we can insert new vertices in the centres of the tiles just described and connect these new vertices trough new edges passing through the face shared by the two vertices. This new net we call the dual of the first net, and if the new net is identical to the first (have the same tiling) we say that this net is self-dual [27]. It is not self-evident, but quite easy to prove, that the dual of a net with transitivity pqrs, has the transitivity srqp. The concept of duals nets is illustrated in Figure 3.

Figure 3. (a) The pcu net transitivity 1111 with its dual net that is an identical pcu net (self-dual); (b) The nbo net in white, transitivity 1111, with its dual the bcu net, also with transitivity 1111. Thus an identical net can easily interpenetrate the pcu net, while this possibility is not obvious for nbo or bcu.

Figure 3. (a) The pcu net transitivity 1111 with its dual net that is an identical pcu net (self-dual); (b) The nbo net in white, transitivity 1111, with its dual the bcu net, also with transitivity 1111. Thus an identical net can easily interpenetrate the pcu net, while this possibility is not obvious for nbo or bcu.

5.2. Interpenetration

The empty space described by the dual nets can often accommodate one or more additional networks, a phenomenon called interpenetration. This was recognized in early work on coordination polymers [28] and the first attempts at classification were made by Batten et al. [29,30]. More recent terminology and nomenclature have been proposed by Proserpio and co-workers based on whether the nets are related by translation, symmetry operations or both. Blatov et al. have also surveyed metal-organic and inorganic 3D networks in the CSD [31].

It should be noted that the description of the interpenetration of 3D-nets is rather straight forward while the possible relations between interpenetrating 2D-nets is much more complex [32,33,34].

It is probably obvious that some nets will be easier to interpenetrate than others, even if it is not proven that self-dual nets actually have a higher ration of interpenetration than other nets [8], so this is a major concern when designing MOFs.

6. Conclusions

The various numerical designators of 3D-nets such as point symbols, vertex symbols and transitivity contain important information for the MOF designer and the three-letter codes from the Reticular Chemistry Structure Resource, RCSR are vital in communicating and discussing MOF structures.