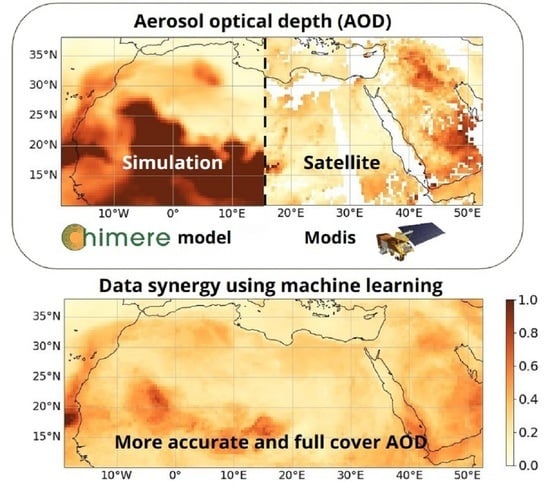
Machine Learning-Based Improvement of Aerosol Optical Depth from CHIMERE Simulations Using MODIS Satellite Observations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Inputs
2.1.1. MODIS Satellite Observations
2.1.2. CHIMERE Simulations
2.1.3. Dataset Preparation
2.2. Bias Correction ML Models Construction
2.2.1. Multiple Linear Regression (MLR)
2.2.2. Feed-Forward Neural Networks (NN)
2.2.3. Random Forest (RF)
2.2.4. Gradient Boosting (XGB)
3. Results and Discussion
3.1. Comparison against Independent MODIS Observations
- a.
- Case study of 30 September 2021
- b.
- Statistical analysis on the testing dataset
- c.
- Prediction of bias corrected AODs at the different daytimes
3.2. Comparison with AERONET Ground-Based Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsikerdekis, A.; Zanis, P.; Georgoulias, A.K.; Alexandri, G.; Katragkou, E.; Karacostas, T.; Solmon, F. Direct and Semi-Direct Radiative Effect of North African Dust in Present and Future Regional Climate Simulations. Clim. Dyn. 2019, 53, 4311–4336. [Google Scholar] [CrossRef]
- Mahowald, N.M.; Baker, A.R.; Bergametti, G.; Brooks, N.; Duce, R.A.; Jickells, T.D.; Kubilay, N.; Prospero, J.M.; Tegen, I. Atmospheric Global Dust Cycle and Iron Inputs to the Ocean. Glob. Biogeochem. Cycles 2005, 19, GB4025. [Google Scholar] [CrossRef]
- Klingmüller, K.; Lelieveld, J.; Karydis, V.A.; Stenchikov, G.L. Direct Radiative Effect of Dust–Pollution Interactions. Atmos. Chem. Phys. 2019, 19, 7397–7408. [Google Scholar] [CrossRef] [Green Version]
- Meng, L.; Zhao, T.; He, Q.; Yang, X.; Mamtimin, A.; Wang, M.; Pan, H.; Huo, W.; Yang, F.; Zhou, C. Dust Radiative Effect Characteristics during a Typical Springtime Dust Storm with Persistent Floating Dust in the Tarim Basin, Northwest China. Remote Sens. 2022, 14, 1167. [Google Scholar] [CrossRef]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The Contribution of Outdoor Air Pollution Sources to Premature Mortality on a Global Scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef] [PubMed]
- Remer, L.A.; Kaufman, Y.J.; Tanré, D.; Mattoo, S.; Chu, D.A.; Martins, J.V.; Li, R.-R.; Ichoku, C.; Levy, R.C.; Kleidman, R.G.; et al. The MODIS Aerosol Algorithm, Products, and Validation. J. Atmos. Sci. 2005, 62, 947–973. [Google Scholar] [CrossRef] [Green Version]
- Menut, L.; Bessagnet, B.; Briant, R.; Cholakian, A.; Couvidat, F.; Mailler, S.; Pennel, R.; Siour, G.; Tuccella, P.; Turquety, S.; et al. The CHIMERE V2020r1 Online Chemistry-Transport Model. Geosci. Model Dev. 2021, 14, 6781–6811. [Google Scholar] [CrossRef]
- Bessagnet, B.; Hodzic, A.; Vautard, R.; Beekmann, M.; Cheinet, S.; Honoré, C.; Liousse, C.; Rouil, L. Aerosol Modeling with CHIMERE—Preliminary Evaluation at the Continental Scale. Atmos. Environ. 2004, 38, 2803–2817. [Google Scholar] [CrossRef]
- Turquety, S.; Menut, L.; Siour, G.; Mailler, S.; Hadji-Lazaro, J.; George, M.; Clerbaux, C.; Hurtmans, D.; Coheur, P.-F. APIFLAME v2.0 Biomass Burning Emissions Model: Impact of Refined Input Parameters on Atmospheric Concentration in Portugal in Summer 2016. Geosci. Model Dev. 2020, 13, 2981–3009. [Google Scholar] [CrossRef]
- Mallet, V.; Sportisse, B. Uncertainty in a Chemistry-Transport Model Due to Physical Parameterizations and Numerical Approximations: An Ensemble Approach Applied to Ozone Modeling. J. Geophys. Res. 2006, 111, D01302. [Google Scholar] [CrossRef]
- Escribano, J.; Boucher, O.; Chevallier, F.; Huneeus, N. Impact of the Choice of the Satellite Aerosol Optical Depth Product in a Sub-Regional Dust Emission Inversion. Atmos. Chem. Phys. 2017, 17, 7111–7126. [Google Scholar] [CrossRef] [Green Version]
- Escribano, J.; Boucher, O.; Chevallier, F.; Huneeus, N. Subregional Inversion of North African Dust Sources. J. Geophys. Res. D Atmos. 2016, 121, 8549–8566. [Google Scholar] [CrossRef] [Green Version]
- Garrigues, S.; Chimot, J.; Ades, M.; Inness, A.; Flemming, J.; Kipling, Z.; Benedetti, A.; Ribas, R.; Jafariserajehlou, S.; Fougnie, B.; et al. Monitoring Multiple Satellite Aerosol Optical Depth (AOD) Products within the Copernicus Atmosphere Monitoring Service (CAMS) Data Assimilation System. Atmos. Clim. Sci. 2022, 22, 14657–14692. [Google Scholar] [CrossRef]
- Bocquet, M.; Elbern, H.; Eskes, H.; Hirtl, M.; Žabkar, R.; Carmichael, G.R.; Flemming, J.; Inness, A.; Pagowski, M.; Pérez Camaño, J.L.; et al. Data Assimilation in Atmospheric Chemistry Models: Current Status and Future Prospects for Coupled Chemistry Meteorology Models. Atmos. Chem. Phys. 2015, 15, 5325–5358. [Google Scholar] [CrossRef] [Green Version]
- Sayeed, A.; Eslami, E.; Lops, Y.; Choi, Y. CMAQ-CNN: A New-Generation of Post-Processing Techniques for Chemical Transport Models Using Deep Neural Networks. Atmos. Environ. 2022, 273, 118961. [Google Scholar] [CrossRef]
- Xu, M.; Jin, J.; Wang, G.; Segers, A.; Deng, T.; Lin, H.X. Machine Learning Based Bias Correction for Numerical Chemical Transport Models. Atmos. Environ. 2021, 248, 118022. [Google Scholar] [CrossRef]
- Jin, J.; Lin, H.X.; Segers, A.; Xie, Y.; Heemink, A. Machine Learning for Observation Bias Correction with Application to Dust Storm Data Assimilation. Chem. Phys. Lipids 2019, 19, 10009–10026. [Google Scholar] [CrossRef] [Green Version]
- Rasp, S.; Lerch, S. Neural Networks for Postprocessing Ensemble Weather Forecasts. Mon. Weather Rev. 2018, 146, 3885–3900. [Google Scholar] [CrossRef] [Green Version]
- Taillardat, M.; Mestre, O.; Zamo, M.; Naveau, P. Calibrated Ensemble Forecasts Using Quantile Regression Forests and Ensemble Model Output Statistics. Mon. Weather Rev. 2016, 144, 2375–2393. [Google Scholar] [CrossRef]
- Nabavi, S.O.; Haimberger, L.; Abbasi, R.; Samimi, C. Prediction of Aerosol Optical Depth in West Asia Using Deterministic Models and Machine Learning Algorithms. Aeolian Res. 2018, 35, 69–84. [Google Scholar] [CrossRef]
- Available online: https://modis.gsfc.nasa.gov/about/specifications.php (accessed on 27 July 2022).
- Sayer, A.M.; Munchak, L.A.; Hsu, N.C.; Levy, R.C.; Bettenhausen, C.; Jeong, M.-J. MODIS Collection 6 Aerosol Products: Comparison between Aqua’s e-Deep Blue, Dark Target, and “Merged” Data Sets, and Usage Recommendations. J. Geophys. Res. 2014, 119, 13965–13989. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Peng, Y.; Sun, L. MODIS Collection 6.1 Aerosol Optical Depth Products over Land and Ocean: Validation and Comparison. Atmos. Environ. 2019, 201, 428–440. [Google Scholar] [CrossRef]
- Gupta, P.; Levy, R.C.; Mattoo, S.; Remer, L.A.; Munchak, L.A. A Surface Reflectance Scheme for Retrieving Aerosol Optical Depth over Urban Surfaces in MODIS Dark Target Retrieval Algorithm. Atmos. Clim. Sci. 2016, 9, 3293–3308. [Google Scholar] [CrossRef] [Green Version]
- Hsu, N.C.; Jeong, M.-J.; Bettenhausen, C.; Sayer, A.M.; Hansell, R.; Seftor, C.S.; Huang, J.; Tsay, S.-C. Enhanced Deep Blue Aerosol Retrieval Algorithm: The Second Generation. J. Geophys. Res. 2013, 118, 9296–9315. [Google Scholar] [CrossRef]
- Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A Federated Instrument Network and Data Archive for Aerosol Characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
- Menut, L.; Bessagnet, B.; Khvorostyanov, D.; Beekmann, M.; Blond, N.; Colette, A.; Coll, I.; Curci, G.; Foret, G.; Hodzic, A.; et al. CHIMERE 2013: A Model for Regional Atmospheric Composition Modelling. Geosci. Model Dev. 2013, 6, 981–1028. [Google Scholar] [CrossRef] [Green Version]
- Available online: http://www.prevair.org/ (accessed on 27 July 2022).
- Ciarelli, G.; Theobald, M.R.; Vivanco, M.G.; Beekmann, M.; Aas, W.; Andersson, C.; Bergström, R.; Manders-Groot, A.; Couvidat, F.; Mircea, M.; et al. Trends of Inorganic and Organic Aerosols and Precursor Gases in Europe: Insights from the EURODELTA Multi-Model Experiment over the 1990--2010 Period. Geosci. Model Dev. 2019, 12, 4923–4954. [Google Scholar] [CrossRef] [Green Version]
- Lachatre, M.; Foret, G.; Laurent, B.; Siour, G.; Cuesta, J.; Dufour, G.; Meng, F.; Tang, W.; Zhang, Q.; Beekmann, M. Air Quality Degradation by Mineral Dust over Beijing, Chengdu and Shanghai Chinese Megacities. Atmosphere 2020, 11, 708. [Google Scholar] [CrossRef]
- Cholakian, A.; Beekmann, M.; Colette, A.; Coll, I.; Siour, G.; Sciare, J.; Marchand, N.; Couvidat, F.; Pey, J.; Gros, V.; et al. Simulation of Fine Organic Aerosols in the Western Mediterranean Area during the ChArMEx 2013 Summer Campaign. Atmos. Clim. Sci. 2018, 18, 7287–7312. [Google Scholar] [CrossRef] [Green Version]
- Deroubaix, A.; Flamant, C.; Menut, L.; Siour, G.; Mailler, S.; Turquety, S.; Briant, R.; Khvorostyanov, D.; Crumeyrolle, S. Interactions of Atmospheric Gases and Aerosols with the Monsoon Dynamics over the Sudano-Guinean Region during AMMA. Atmos. Clim. Sci. 2018, 18, 445–465. [Google Scholar] [CrossRef] [Green Version]
- Fortems-Cheiney, A.; Dufour, G.; Foret, G.; Siour, G.; Van Damme, M.; Coheur, P.-F.; Clarisse, L.; Clerbaux, C.; Beekmann, M. Understanding the Simulated Ammonia Increasing Trend from 2008 to 2015 over Europe with CHIMERE and Comparison with IASI Observations. Atmosphere 2022, 13, 1101. [Google Scholar] [CrossRef]
- Mailler, S.; Menut, L.; Khvorostyanov, D.; Valari, M.; Couvidat, F.; Siour, G.; Turquety, S.; Briant, R.; Tuccella, P.; Bessagnet, B.; et al. CHIMERE-2017: From Urban to Hemispheric Chemistry-Transport Modeling. Geosci. Model Dev. 2017, 10, 2397–2423. [Google Scholar] [CrossRef] [Green Version]
- Bian, H.; Prather, M.J. Fast-J2: Accurate Simulation of Stratospheric Photolysis in Global Chemical Models. J. Atmos. Chem. 2002, 41, 281–296. [Google Scholar] [CrossRef]
- Péré, J.C.; Mallet, M.; Pont, V.; Bessagnet, B. Evaluation of an Aerosol Optical Scheme in the Chemistry-Transport Model CHIMERE. Atmos. Environ. 2010, 44, 3688–3699. [Google Scholar] [CrossRef]
- Hauglustaine, D.A.; Hourdin, F.; Jourdain, L.; Filiberti, M.-A.; Walters, S.; Lamarque, J.-F.; Holland, E.A. Interactive Chemistry in the Laboratoire de Météorologie Dynamique General Circulation Model: Description and Background Tropospheric Chemistry Evaluation. J. Geophys. Res. D Atmos. 2004, 109, D04314. [Google Scholar] [CrossRef]
- Skamarock, C.; Klemp, B.; Dudhia, J.; Gill, O.; Liu, Z.; Berner, J.; Wang, W.; Powers, G.; Duda, G.; Barker, D.; et al. A Description of the Advanced Research WRF Model Version 4.1; National Center for Atmospheric Research (NCAR): Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
- Derognat, C.; Beekmann, M.; Baeumle, M.; Martin, D.; Schmidt, H. Effect of Biogenic Volatile Organic Compound Emissions on Tropospheric Chemistry during the Atmospheric Pollution Over the Paris Area (ESQUIF) Campaign in the Ile-de-France Region. J. Geophys. Res. 2003, 108, 8560. [Google Scholar] [CrossRef]
- Monica, C.; Diego, G.; Marilena, M.; Edwin, S.; Gabriel, O. EDGAR v5.0 Global Air Pollutant Emissions. European Commission, Joint Research Centre (JRC) [Dataset] PID. 2019. Available online: http://data.europa.eu/89h/377801af-b094-4943-8fdc-f79a7c0c2d19 (accessed on 5 March 2023).
- Alfaro, S.C.; Gomes, L. Modeling Mineral Aerosol Production by Wind Erosion: Emission Intensities and Aerosol Size Distributions in Source Areas. J. Geophys. Res. Atmos. 2001, 106, 18075–18084. [Google Scholar] [CrossRef]
- Menut, L.; Schmechtig, C.; Marticorena, B. Sensitivity of the Sandblasting Flux Calculations to the Soil Size Distribution Accuracy. J. Atmos. Ocean. Technol. 2005, 22, 1875–1884. [Google Scholar] [CrossRef]
- Gama, C.; Ribeiro, I.; Lange, A.C.; Vogel, A.; Ascenso, A.; Seixas, V.; Elbern, H.; Borrego, C.; Friese, E.; Monteiro, A. Performance Assessment of CHIMERE and EURAD-IM’ Dust Modules. Atmos. Pollut. Res. 2019, 10, 1336–1346. [Google Scholar] [CrossRef]
- Menut, L.; Chiapello, I.; Moulin, C. Previsibility of Saharan Dust Events Using the CHIMERE-DUST Transport Model. IOP Conf. Ser. Earth Environ. Sci. 2009, 7, 012009. [Google Scholar] [CrossRef]
- Chaibou, A.A.; Ma, X.; Kumar, K.R.; Jia, H.; Tang, Y.; Sha, T. Evaluation of Dust Extinction and Vertical Profiles Simulated by WRF-Chem with CALIPSO and AERONET over North Africa. J. Atmos. Sol. Terr. Phys. 2020, 199, 105213. [Google Scholar] [CrossRef]
- Washington, R.; Bouet, C.; Cautenet, G.; Mackenzie, E.; Ashpole, I.; Engelstaedter, S.; Lizcano, G.; Henderson, G.M.; Schepanski, K.; Tegen, I. Dust as a Tipping Element: The Bodélé Depression, Chad. Proc. Natl. Acad. Sci. USA 2009, 106, 20564–20571. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bellman, R. Adaptive Control Processes. A Guided Tour; Princeton University Press: Princeton, NJ, USA, 1961; p. 276. [Google Scholar]
- Available online: https://www.python.org/ (accessed on 22 July 2022).
- Available online: https://jupyterbook.org (accessed on 22 July 2022).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. 2011, 12, 2825–2830. [Google Scholar]
- Bengio, Y. Learning Deep Architectures for AI. Found. Trends® Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- MacKay, D.J.C. A Practical Bayesian Framework for Backpropagation Networks. Neural Comput. 1992, 4, 448–472. [Google Scholar] [CrossRef] [Green Version]
- Dubey, S.R.; Singh, S.K.; Chaudhuri, B.B. Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark. Neurocomputing 2022, 503, 92–108. [Google Scholar] [CrossRef]
- Dauphin, Y.N.; Pascanu, R.; Gulcehre, C.; Cho, K.; Ganguli, S.; Bengio, Y. Identifying and Attacking the Saddle Point Problem in High-Dimensional Non-Convex Optimization. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, USA, 8–13 December 2014. [Google Scholar]
- Goodfellow, I.J.; Vinyals, O.; Saxe, A.M. Qualitatively Characterizing Neural Network Optimization Problems. arXiv 2014, arXiv:1412.6544. [Google Scholar]
- Zhou, Y.; Yang, J.; Zhang, H.; Liang, Y.; Tarokh, V. SGD Converges to Global Minimum in Deep Learning via Star-Convex Path. arXiv 2019, arXiv:1901.00451. [Google Scholar]
- Du, S.; Lee, J.; Li, H.; Wang, L.; Zhai, X. Gradient Descent Finds Global Minima of Deep Neural Networks. In Proceedings of the 36th International Conference on Machine Learning (PMLR, 92019), Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 1675–1685. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. 2019. Available online: https://github.com/keras-team/keras-tuner (accessed on 5 March 2023).
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the 32nd International Conference on Machine Learning (PMLR), Lille, France, 7–9 July 2015; Volume 37, pp. 448–456. [Google Scholar]
- Fukushima, K. Cognitron: A Self-Organizing Multilayered Neural Network. Biol. Cybern. 1975, 20, 121–136. [Google Scholar] [CrossRef]
- Hinton, G.E.; Srivastava, N.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R.R. Improving Neural Networks by Preventing Co-Adaptation of Feature Detectors. arXiv 2012, arXiv:1207.0580. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Breiman, L. Randomizing outputs to increase prediction accuracy. Mach. Learn. 2000, 40, 229–242. [Google Scholar] [CrossRef] [Green Version]
- Gordon, A.D.; Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees. Biometrics 1984, 40, 874. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar]
- Olson, R.S.; Moore, J.H. TPOT: A Tree-Based Pipeline Optimization Tool for Automating Machine Learning. In Proceedings of the Workshop on Automatic Machine Learning (PMLR), New York, NY, USA, 24 June 2016; Volume 64, pp. 66–74. [Google Scholar]
- Available online: https://xgboost.readthedocs.io/en/stable/parameter.html (accessed on 2 August 2022).
- Cuesta, J.; Flamant, C.; Gaetani, M.; Knippertz, P.; Fink, A.H.; Chazette, P.; Eremenko, M.; Dufour, G.; Di Biagio, C.; Formenti, P. Three-dimensional Pathways of Dust over the Sahara during Summer 2011 as Revealed by New Infrared Atmospheric Sounding Interferometer Observations. Q. J. R. Meteorol. Soc. 2020, 146, 2731–2755. [Google Scholar] [CrossRef]
- Worldview: Explore Your Dynamic Planet. Available online: https://worldview.earthdata.nasa.gov/ (accessed on 31 January 2023).
- Xu, K.; Zhang, M.; Li, J.; Du, S.S.; Kawarabayashi, K.-I.; Jegelka, S. How Neural Networks Extrapolate: From Feedforward to Graph Neural Networks. arXiv 2020, arXiv:2009.11848. [Google Scholar]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. arXiv 2017, arXiv:1705.07874. [Google Scholar]
- Drake, N.; Bristow, C. Shorelines in the Sahara: Geomorphological Evidence for an Enhanced Monsoon from Palaeolake Megachad. Holocene 2006, 16, 901–911. [Google Scholar] [CrossRef]
- Chudnovsky, A.; Kostinski, A.; Herrmann, L.; Koren, I.; Nutesku, G.; Ben-Dor, E. Hyperspectral Spaceborne Imaging of Dust-Laden Flows: Anatomy of Saharan Dust Storm from the Bodélé Depression. Remote Sens. Environ. 2011, 115, 1013–1024. [Google Scholar] [CrossRef]
- Hsu, N.C.; Tsay, S.-C.; King, M.D.; Herman, J.R. Aerosol Properties over Bright-Reflecting Source Regions. IEEE Trans. Geosci. Remote Sens. 2004, 42, 557–569. [Google Scholar] [CrossRef]
- Rocha-Lima, A.; Martins, J.V.; Remer, L.A.; Todd, M.; Marsham, J.H.; Engelstaedter, S.; Ryder, C.L.; Cavazos-Guerra, C.; Artaxo, P.; Colarco, P.; et al. A Detailed Characterization of the Saharan Dust Collected during the Fennec Campaign in 2011: In Situ Ground-Based and Laboratory Measurements. Atmos. Clim. Sci. 2018, 18, 1023–1043. [Google Scholar] [CrossRef] [Green Version]
- Todd, M.C.; Washington, R.; Martins, J.V.; Dubovik, O.; Lizcano, G.; M’Bainayel, S.; Engelstaedter, S. Mineral Dust Emission from the Bodélé Depression, Northern Chad, during BoDEx 2005. J. Geophys. Res. 2007, 112, D06207. [Google Scholar] [CrossRef]
- Cuesta, J.; Eremenko, M.; Flamant, C.; Dufour, G.; Laurent, B.; Bergametti, G.; Höpfner, M.; Orphal, J.; Zhou, D. Three-Dimensional Distribution of a Major Desert Dust Outbreak over East Asia in March 2008 Derived from IASI Satellite Observations. J. Geophys. Res. Atmos. 2015, 120, 7099–7127. [Google Scholar] [CrossRef] [Green Version]
- Lemmouchi, F.; Cuesta, J.; Eremenko, M.; Derognat, C.; Siour, G.; Dufour, G.; Sellitto, P.; Turquety, S.; Tran, D.; Liu, X.; et al. Three-Dimensional Distribution of Biomass Burning Aerosols from Australian Wildfires Observed by TROPOMI Satellite Observations. Remote Sens. 2022, 14, 2582. [Google Scholar] [CrossRef]













| t(s) | r | RMSE | MAE | Skp | μ | Min | 25% | 50% | 75% | Max | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| RAW | N/A | 0.56 | 0.65 | 0.37 | 2.55 | 0.24 | −3.57 | −0.09 | 0.03 | 0.39 | 6.95 |
| MLR | 0.19 | 0.62 | 0.21 | 0.13 | −3.9 | 0 | −4.15 | −0.06 | 0.03 | 0.1 | 2.49 |
| NN | 0.35 | 0.69 | 0.19 | 0.12 | −3.18 | 0 | −4.04 | −0.06 | 0.02 | 0.09 | 5.09 |
| RF | 0.22 | 0.71 | 0.19 | 0.12 | −3.45 | 0.01 | −4.21 | −0.05 | 0.03 | 0.1 | 2 |
| XGB | 0.3 | 0.71 | 0.19 | 0.12 | −2.93 | 0.01 | −3.96 | −0.06 | 0.02 | 0.09 | 2.47 |
| r | RMSE | MAE | MB | |
|---|---|---|---|---|
| RAW | 0.52 | 0.59 | 0.34 | −0.23 |
| RF-corrected | 0.68 | 0.19 | 0.12 | −0.03 |
| r | RMSE | MAE | MB | |
|---|---|---|---|---|
| MODIS | 0.85 | 0.12 | 0.09 | 0.03 |
| RAW | 0.54 | 0.45 | 0.27 | 0.18 |
| RF | 0.73 | 0.16 | 0.12 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lemmouchi, F.; Cuesta, J.; Lachatre, M.; Brajard, J.; Coman, A.; Beekmann, M.; Derognat, C. Machine Learning-Based Improvement of Aerosol Optical Depth from CHIMERE Simulations Using MODIS Satellite Observations. Remote Sens. 2023, 15, 1510. https://doi.org/10.3390/rs15061510
Lemmouchi F, Cuesta J, Lachatre M, Brajard J, Coman A, Beekmann M, Derognat C. Machine Learning-Based Improvement of Aerosol Optical Depth from CHIMERE Simulations Using MODIS Satellite Observations. Remote Sensing. 2023; 15(6):1510. https://doi.org/10.3390/rs15061510
Chicago/Turabian StyleLemmouchi, Farouk, Juan Cuesta, Mathieu Lachatre, Julien Brajard, Adriana Coman, Matthias Beekmann, and Claude Derognat. 2023. "Machine Learning-Based Improvement of Aerosol Optical Depth from CHIMERE Simulations Using MODIS Satellite Observations" Remote Sensing 15, no. 6: 1510. https://doi.org/10.3390/rs15061510