A Satellite-Based Tool for Mapping Evaporation in Inland Water Bodies: Formulation, Application, and Operational Aspects
Abstract
:1. Introduction
| Model | Name | Methodology | Input Variables | Strengths | Constrains | References |
|---|---|---|---|---|---|---|
| Simplified | Stephens–Stewart Makkink, Doorenbos–Pruitt, Jensen–Haise | Empirical relations between evaporation and solar radiation | Air temperature, solar radiation | Very low data demand If properly tuned, they can provide cost-effective evaporation estimates | Site-specific, they require some empirical coefficients to be calibrated | [36,37,38,39] |
| Blaney–Criddle, | Empirical relations between evaporation and daylight hours | Air temperature, daylight hours | [16,36,40] | |||
| Papadakis, Thornthwaite | ||||||
| Mass balance | Calculates the water budget of the water body | Inflows, rainfall, runoff, outflows, water levels | Very accurate if the water budget is properly closed | Extremely data demanding Require continuous and accurate measurements of the input variables | e.g., [41] | |
| Energy budget | BREB RS-based (SEBAL, METRIC, SEBS, AquaSEBS) | Calculate all the energy contributions entering and exiting the water body | Solar radiation, water temperature, air temperature, wind speed, relative humidity | Provide a comprehensive description of the energy balance. If RS-based, they provide evaporation maps | Data demanding | [13,17,31,42] [25,27,28,33] |
| Mass transfer or bulk transfer | Dalton’s law (Dalton 1802) | Water temperature, air temperature, wind speed, relative humidity | Low data demand | Requires the tuning of the wind function | e.g., [43] | |
| Combined | Priestly–Taylor, de Bruin, Brutsaert and Sticker, Penman | Combine radiative and aerodynamic terms | All variables required by the energy budget and mass transfer models | Most accurate Consider the energy stored by the water body | Most data demanding | [44,45,46,47,48] |
2. Materials and Methods
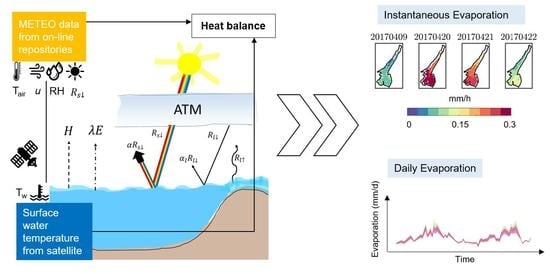
2.1. The LakeVap Tool
2.1.1. Formulation
2.1.2. Inputs and Outputs of the Model
- Water temperature , from now on referred to as Lake Surface Water Temperature (LSWT) from EO data at the satellite overpass time (i.e., between 9:30 and 10:30 UTC in the CCI-Lakes dataset). We took 10:00 UTC as a reference time;
- Downward shortwave radiation ;
- Air temperature ;
- Wind speed ;
- Relative humidity .
- Maps of instantaneous evaporation () at satellite overpass;
- Maps of daily evaporation () estimated during the 24 h including and after the satellite overpass (e.g., from 10:00 UTC to 09:00 UTC of the following day based on the CCI-Lakes dataset reference time). Daily evaporation is obtained by summing the hourly values estimated over the 24 h from the satellite overpass time.
2.2. Study Site
2.3. Data
2.3.1. Remote Sensing Imagery from CCI-Lakes Database
2.3.2. Meteorological Data
2.3.3. Delft3D Hydro-Thermodynamic Model
2.4. LakeVap Tool Runs and Evaluation Metrics
- LakeVap tool fed with WRF meteorological data (spatial average of grid points over the lake surface) from 2004 to 2018 (Section 3.1, Section 3.2 and Section 3.3);
- LakeVap tool fed with MET1 meteorological data (single-point values) from 1995 to 2019 (Section 3.2 and Section 3.3);
- LakeVap tool fed with MET2 meteorological data (single-point values) from 2012 to 2018 (Section 3.2 and Section 3.3);
- LakeVap tool fed with ERA5 meteorological data (spatial average of grid points over the lake surface) from 1995 to 2019 (Section 3.2 and Section 3.3).
- 5.
- LakeVap tool fed by WRF meteorological data spatially averaged over the lake surface (i.e., item 1. in the previous list, taken as reference);
- 6.
- Three sets where one of the three atmospheric variables is imposed as spatially varying at the time (e.g., air temperature), while the other two (e.g., wind speed and relative humidity) are kept as uniform over the lake (from a spatial average of WRF fields);
- 7.
- Three sets where pairs of atmospheric variables are given as spatially varying (air temperature and wind, relative humidity and wind, air temperature and relative humidity), while the remaining one is kept as uniform over the lake (from a spatial average of WRF fields);
- 8.
- LakeVap tool fed by all atmospheric fields from WRF.
3. Results
3.1. Long Term Evaporation Estimates
3.2. Validation of LakeVap Products with Delft3D Outputs
3.3. Implications of the Use of Different Meteorological Datasets
3.4. Spatial Variability of Evaporation
4. Discussion
4.1. Evaporation Estimates for Lake Garda
4.2. Sensitivity to Meteorological Forcing and Morphological Complexity of the Test Site
4.3. The LakeVap Tool and Applicability to Other Lakes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Code Availability
References
- Wang, W.; Lee, X.; Xiao, W.; Liu, S.; Schultz, N.; Wang, Y.; Zhang, M.; Zhao, L. Global Lake Evaporation Accelerated by Changes in Surface Energy Allocation in a Warmer Climate. Nat. Geosci. 2018, 11, 410–414. [Google Scholar] [CrossRef]
- Woolway, R.I.; Merchant, C.J.; Van Den Hoek, J.; Azorin-Molina, C.; Nõges, P.; Laas, A.; Mackay, E.B.; Jones, I.D. Northern Hemisphere Atmospheric Stilling Accelerates Lake Thermal Responses to a Warming World. Geophys. Res. Lett. 2019, 46, 11983–11992. [Google Scholar] [CrossRef] [Green Version]
- Vystavna, Y.; Harjung, A.; Monteiro, L.R.; Matiatos, I.; Wassenaar, L.I. Stable Isotopes in Global Lakes Integrate Catchment and Climatic Controls on Evaporation. Nat. Commun. 2021, 12, 7224. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Wang, L.; Li, D.; Leung, L.R. Spatial Pattern of Lake Evaporation Increases under Global Warming Linked to Regional Hydroclimate Change. Commun. Earth Environ. 2021, 2, 255. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated World Map of the Köppen-Geiger Climate Classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Maberly, S.C.; O’Donnell, R.A.; Woolway, R.I.; Cutler, M.E.J.; Gong, M.; Jones, I.D.; Merchant, C.J.; Miller, C.A.; Politi, E.; Scott, E.M.; et al. Global Lake Thermal Regions Shift under Climate Change. Nat. Commun. 2020, 11, 1232. [Google Scholar] [CrossRef]
- Riveros-Iregui, D.A.; Lenters, J.D.; Peake, C.S.; Ong, J.B.; Healey, N.C.; Zlotnik, V.A. Evaporation from a Shallow, Saline Lake in the Nebraska Sandhills: Energy Balance Drivers of Seasonal and Interannual Variability. J. Hydrol. 2017, 553, 172–187. [Google Scholar] [CrossRef] [Green Version]
- Blanken, P.D.; Spence, C.; Hedstrom, N.; Lenters, J.D. Evaporation from Lake Superior: 1. Physical Controls and Processes. J. Great Lakes Res. 2011, 37, 707–716. [Google Scholar] [CrossRef]
- Xiao, K.; Griffis, T.J.; Baker, J.M.; Bolstad, P.V.; Erickson, M.D.; Lee, X.; Wood, J.D.; Hu, C.; Nieber, J.L. Evaporation from a Temperate Closed-Basin Lake and Its Impact on Present, Past, and Future Water Level. J. Hydrol. 2018, 561, 59–75. [Google Scholar] [CrossRef]
- Yang, K.; Lu, H.; Yue, S.; Zhang, G.; Lei, Y.; La, Z.; Wang, W. Quantifying Recent Precipitation Change and Predicting Lake Expansion in the Inner Tibetan Plateau. Clim. Chang. 2018, 147, 149–163. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, Y.; Ma, N.; Xu, J.; Zhang, T. Long-Term Changes in Evaporation over Siling Co Lake on the Tibetan Plateau and Its Impact on Recent Rapid Lake Expansion. Atmos. Res. 2019, 216, 141–150. [Google Scholar] [CrossRef]
- Elsawwaf, M.; Willems, P.; Feyen, J. Assessment of the Sensitivity and Prediction Uncertainty of Evaporation Models Applied to Nasser Lake, Egypt. J. Hydrol. 2010, 395, 10–22. [Google Scholar] [CrossRef]
- Bozorgi, A.; Bozorg-Haddad, O.; Sima, S.; Loáiciga, H.A. Comparison of Methods to Calculate Evaporation from Reservoirs. Int. J. River Basin Manag. 2020, 18, 1–12. [Google Scholar] [CrossRef]
- Friedrich, K.; Grossman, R.L.; Huntington, J.; Blanken, P.D.; Lenters, J.; Holman, K.D.; Gochis, D.; Livneh, B.; Prairie, J.; Skeie, E.; et al. Reservoir Evaporation in the Western United States: Current Science, Challenges, and Future Needs. Bull. Am. Meteorol. Soc. 2018, 99, 167–187. [Google Scholar] [CrossRef]
- Sene, K.; Gash, J.; McNeil, D. Evaporation from a Tropical Lake: Comparison of Theory with Direct Measurements. J. Hydrol. 1991, 127, 193–217. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; Winter, T.C.; Buso, D.C.; Likens, G.E. Comparison of 15 Evaporation Methods Applied to a Small Mountain Lake in the Northeastern USA. J. Hydrol. 2007, 340, 149–166. [Google Scholar] [CrossRef]
- Ali, S.; Ghosh, N.C.; Singh, R. Evaluating Best Evaporation Estimate Model for Water Surface Evaporation in Semi-Arid Region, India. Hydrol. Process 2008, 22, 1093–1106. [Google Scholar] [CrossRef]
- Alazard, M.; Leduc, C.; Travi, Y.; Boulet, G.; Ben Salem, A. Estimating Evaporation in Semi-Arid Areas Facing Data Scarcity: Example of the El Haouareb Dam (Merguellil Catchment, Central Tunisia). J. Hydrol. Reg. Stud. 2015, 3, 265–284. [Google Scholar] [CrossRef] [Green Version]
- Majidi, M.; Alizadeh, A.; Farid, A.; Vazifedoust, M. Development and Application of a New Lake Evaporation Estimation Approach Based on Energy Balance. Hydrol. Res. 2018, 49, 1528–1539. [Google Scholar] [CrossRef]
- Lowe, L.D.; Webb, J.A.; Nathan, R.J.; Etchells, T.; Malano, H.M. Evaporation from Water Supply Reservoirs: An Assessment of Uncertainty. J. Hydrol. 2009, 376, 261–274. [Google Scholar] [CrossRef]
- Wang, W.; Xiao, W.; Cao, C.; Gao, Z.; Hu, Z.; Liu, S.; Shen, S.; Wang, L.; Xiao, Q.; Xu, J.; et al. Temporal and Spatial Variations in Radiation and Energy Balance across a Large Freshwater Lake in China. J. Hydrol. 2014, 511, 811–824. [Google Scholar] [CrossRef]
- Rahaghi, A.I.; Lemmin, U.; Cimatoribus, A.; Bouffard, D.; Riffler, M.; Wunderle, S.; Barry, D.A. Improving Surface Heat Flux Estimation for a Large Lake through Model Optimization and Two-Point Calibration: The Case of Lake Geneva. Limnol. Oceanogr. Methods 2018, 16, 576–593. [Google Scholar] [CrossRef]
- Spence, C.; Blanken, P.D.; Hedstrom, N.; Fortin, V.; Wilson, H. Evaporation from Lake Superior: 2. Spatial Distribution and Variability. J. Great Lakes Res. 2011, 37, 717–724. [Google Scholar] [CrossRef]
- Rahaghi, A.I.; Lemmin, U.; Cimatoribus, A.A.; Barry, D.A. The Importance of Systematic Spatial Variability in the Surface Heat Flux of a Large Lake: A Multiannual Analysis for Lake Geneva. Water Resour. Res. 2019, 55, 10248–10267. [Google Scholar] [CrossRef] [Green Version]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, Y.; Moreno, J.F.; Roerink, G.J.; Van Der Wal, T. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL).: Part 2: Validation. J. Hydrol. 1998, 212–213, 213–229. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.L.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Amayreh, J. DigitalCommons @ USU All Graduate Theses and Dissertations Lake Evaporation: A Model Study. 1995. Available online: https://digitalcommons.usu.edu/etd/4404 (accessed on 28 April 2022).
- Hassan, M. Evaporation Estimation for Lake Nasser Based on Remote Sensing Technology. Ain Shams Eng. J. 2013, 4, 593–604. [Google Scholar] [CrossRef] [Green Version]
- Zamani Losgedaragh, S.; Rahimzadegan, M. Evaluation of SEBS, SEBAL, and METRIC Models in Estimation of the Evaporation from the Freshwater Lakes (Case Study: Amirkabir Dam, Iran). J. Hydrol. 2018, 561, 523–531. [Google Scholar] [CrossRef]
- Abdelrady, A.; Timmermans, J.; Vekerdy, Z.; Salama, M.S. Surface Energy Balance of Fresh and Saline Waters: AquaSEBS. Remote Sens. 2016, 8, 583. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Gao, H. Estimating Reservoir Evaporation Losses for the United States: Fusing Remote Sensing and Modeling Approaches. Remote Sens. Environ. 2019, 226, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Amadori, M.; Giovannini, L.; Toffolon, M.; Piccolroaz, S.; Zardi, D.; Bresciani, M.; Giardino, C.; Luciani, G.; Kliphuis, M.; van Haren, H.; et al. Multi-Scale Evaluation of a 3D Lake Model Forced by an Atmospheric Model against Standard Monitoring Data. Environ. Model. Softw. 2021, 139, 105017. [Google Scholar] [CrossRef]
- McGuinness, J.L.; Bordne, E.F. A Comparison of Lysimeter-Derived Potential Evapotranspiration with Computed Values; U.S. Department of Agriculture: Washington, DC, USA, 1972; Volume Technical.
- Hargreaves, G.H. Moisture Availability and Crop Production. Trans. ASAE 1975, 18, 0980–0984. [Google Scholar] [CrossRef]
- Delclaux, F.; Coudrain, A.; Condom, T. Evaporation Estimation on Lake Titicaca: A Synthesis Review and Modelling. Hydrol. Process 2007, 21, 1664–1677. [Google Scholar] [CrossRef]
- Ward, A.D.; Trimble, S.W. Environmental Hydrology; Lewis: Boca Raton, FL, USA, 2003. [Google Scholar]
- Hamon, W.R. Estimating Potential Evapotranspiration. J. Hydraul. Div. 1961, 87, 107–120. [Google Scholar] [CrossRef]
- Hassani, A. Thermal Structure and Energy Budget for Alghadir Reservoir, Iran. Water Resour. 2013, 40, 621–630. [Google Scholar] [CrossRef]
- Aydin, H.; Karakuş, H. Estimation of Evaporation for Lake Van. Environ. Earth Sci. 2016, 75, 1275. [Google Scholar] [CrossRef]
- Singh, V.P.; Xu, C.-Y. Evaluation and Generalization of 13 Mass-Transfer Equations for Determining Free Water Evaporation. Hydrol. Process 1997, 11, 311–323. [Google Scholar] [CrossRef]
- Stewart, R.B.; Rouse, W.R. A Simple Method for Determining the Evaporation from Shallow Lakes and Ponds. Water Resour. Res. 1976, 12, 623–628. [Google Scholar] [CrossRef]
- De Bruin, H.A.R. A Simple Model for Shallow Lake Evaporation. J. Appl. Meteorol. 1978, 17, 1132–1134. [Google Scholar] [CrossRef] [Green Version]
- De Bruin, H.A.R.; Keijman, J.Q. The Priestley-Taylor Evaporation Model Applied to a Large, Shallow Lake in the Netherlands. J. Appl. Meteorol. 1979, 18, 898–903. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W.; Stricker, H. An Advection-Aridity Approach to Estimate Actual Regional Evapotranspiration. Water Resour. Res. 1979, 15, 443–450. [Google Scholar] [CrossRef]
- Brutsaert, W. Evaporation into the Atmosphere; Springer: Dordrecht, The Netherlands, 1982; ISBN 978-90-481-8365-4. [Google Scholar]
- Fink, G.; Schmid, M.; Wahl, B.; Wolf, T.; Wüest, A. Heat Flux Modifications Related to Climate-Induced Warming of Large European Lakes. Water Resour. Res. 2014, 50, 2072–2085. [Google Scholar] [CrossRef] [Green Version]
- Livingstone, D.M.; Imboden, D.M. Annual Heat Balance and Equilibrium Temperature of Lake Aegeri, Switzerland. Aquat. Sci. 1989, 51, 351–369. [Google Scholar] [CrossRef]
- Gianniou, S.K.; Antonopoulos, V.Z. Evaporation and Energy Budget in Lake Vegoritis, Greece. J. Hydrol. 2007, 345, 212–223. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Serafin, S.; Zardi, D. The Thermally Driven Diurnal Wind System of the Adige Valley in the Italian Alps. Q. J. R. Meteorol. Soc. 2017, 143, 2389–2402. [Google Scholar] [CrossRef]
- Ambrosetti, W.; Barbanti, L. Deep Water Warming in Lakes: An Indicator of Climatic Change. J. Limnol. 1999, 58, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Salmaso, N. Effects of Climatic Fluctuations and Vertical Mixing on the Interannual Trophic Variability of Lake Garda, Italy. Limnol. Oceanogr. 2005, 50, 553–565. [Google Scholar] [CrossRef]
- Piccolroaz, S.; Amadori, M.; Toffolon, M.; Dijkstra, H.A. Importance of Planetary Rotation for Ventilation Processes in Deep Elongated Lakes: Evidence from Lake Garda (Italy). Sci. Rep. 2019, 9, 8290. [Google Scholar] [CrossRef] [PubMed]
- Biemond, B.; Amadori, M.; Toffolon, M.; Piccolroaz, S.; Van Haren, H.; Dijkstra, H.A. Deep-Mixing and Deep-Cooling Events in Lake Garda: Simulation and Mechanisms. J. Limnol. 2021, 80. [Google Scholar] [CrossRef]
- Amadori, M.; Zamparelli, V.; De Carolis, G.; Fornaro, G.; Toffolon, M.; Bresciani, M.; Giardino, C.; De Santi, F. Monitoring Lakes Surface Water Velocity with SAR: A Feasibility Study on Lake Garda, Italy. Remote Sens. 2021, 13, 2293. [Google Scholar] [CrossRef]
- Pareeth, S.; Salmaso, N.; Adrian, R.; Neteler, M. Homogenised Daily Lake Surface Water Temperature Data Generated from Multiple Satellite Sensors: A Long-Term Case Study of a Large Sub-Alpine Lake. Sci. Rep. 2016, 6, 31251. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giovannini, L.; Antonacci, G.; Zardi, D.; Laiti, L.; Panziera, L. Sensitivity of Simulated Wind Speed to Spatial Resolution over Complex Terrain. Energy Procedia 2014, 59, 323–329. [Google Scholar] [CrossRef] [Green Version]
- Giardino, C.; Bresciani, M.; Cazzaniga, I.; Schenk, K.; Rieger, P.; Braga, F.; Matta, E.; Brando, V.E. Evaluation of Multi-Resolution Satellite Sensors for Assessing Water Quality and Bottom Depth of Lake Garda. Sensors 2014, 14, 24116–24131. [Google Scholar] [CrossRef] [Green Version]
- Simis, S.; Selmes, N.; Calmettes, B.; Duguay, C.; Merchant, C.J.; Malnes, E.; Ye´sou, H.; Blanco, P. D4.3: Product User Guide (PUG). 2020. Available online: https://climate.esa.int/en/projects/lakes/key-documents-lakes/ (accessed on 21 April 2022).
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1981 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). Available online: https://doi.org/10.24381/cds.e2161bac (accessed on 21 April 2022).
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.; Duda, M.G.; Huang, X.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; (No. NCAR/TN-475+STR); University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Lawrence, M.G. The Relationship between Relative Humidity and the Dewpoint Temperature in Moist Air: A Simple Conversion and Applications. Bull. Am. Meteorol. Soc. 2005, 86, 225–234. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and Validation of a Three-Dimensional Morphological Model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Ghirardi, N.; Amadori, M.; Free, G.; Giovannini, L.; Toffolon, M.; Giardino, C.; Bresciani, M. Using Remote Sensing and Numerical Modelling to Quantify a Turbidity Discharge Event in Lake Garda. J. Limnol. 2020, 80. [Google Scholar] [CrossRef]
- Vercauteren, N.; Bou-Zeid, E.; Huwald, H.; Parlange, M.B.; Brutsaert, W. Estimation of Wet Surface Evaporation from Sensible Heat Flux Measurements. Water Resour. Res. 2009, 45, W06424. [Google Scholar] [CrossRef] [Green Version]
- Lenters, J.D.; Kratz, T.K.; Bowser, C.J. Effects of Climate Variability on Lake Evaporation: Results from a Long-Term Energy Budget Study of Sparkling Lake, Northern Wisconsin (USA). J. Hydrol. 2005, 308, 168–195. [Google Scholar] [CrossRef]
- Crétaux, J.-F.; Merchant, C.J.; Duguay, C.; Simis, S.; Calmettes, B.; Bergé-Nguyen, M.; Wu, Y.; Zhang, D.; Carrea, L.; Liu, X.; et al. ESA Lakes Climate Change Initiative (Lakes_cci): Lake Products, Version 1.0; Centre for Environmental Data Analysis: Chilton, UK, 2020. [Google Scholar] [CrossRef]
- Kuhn, W. Aus Wärmehaushalt Und Klimadaten Berechnete Verdunstung des Zürichsees. Naturf. Ges. Zürich Orell Füssli 1978, 123, 261–283. [Google Scholar]
- Mekonnen, M.M.; Hoekstra, A.Y. The Blue Water Footprint of Electricity from Hydropower. Hydrol. Earth Syst. Sci. 2012, 16, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Ramamurthy, P.; Bou-Zeid, E. Heatwaves and Urban Heat Islands: A Comparative Analysis of Multiple Cities. J. Geophys. Res. Atmos. 2017, 122, 168–178. [Google Scholar] [CrossRef]
- Ranasinghe. Climate Change Information for Regional Impact and for Risk Assessment: Chapter 12; Cambridge University Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Gupta, N.; Mathew, A.; Khandelwal, S. Analysis of Cooling Effect of Water Bodies on Land Surface Temperature in Nearby Region: A Case Study of Ahmedabad and Chandigarh Cities in India. Egypt. J. Remote Sens. Space Sci. 2019, 22, 81–93. [Google Scholar] [CrossRef]
- Ghirardi, N.; Bresciani, M.; Free, G.; Pinardi, M.; Bolpagni, R.; Giardino, C. Evaluation of Macrophyte Community Dynamics (2015–2020) in Southern Lake Garda (Italy) from Sentinel-2 Data. Appl. Sci. 2022, 12, 2693. [Google Scholar] [CrossRef]
- Longoni, V.; Fasola, M. Le Popolazioni di Uccelli Acquatici Svernanti in Lombardia, 2019 International Waterbird Census 2019; Regione Lombardia: Milan, Italy, 2020. [Google Scholar]
- Wukelic, G.E.; Gibbons, D.E.; Martucci, L.M.; Foote, H.P. Radiometric Calibration of Landsat Thematic Mapper Thermal Band. Remote Sens. Environ. 1989, 28, 339–347. [Google Scholar] [CrossRef]
- Brutsaert, W. On a Derivable Formula for Long-Wave Radiation from Clear Skies. Water Resour. Res. 1975, 11, 742–744. [Google Scholar] [CrossRef]








| Type of Data | Time Availability | ID | Data Provider | Frequency | Spatial Resolution |
|---|---|---|---|---|---|
| LSWT maps | 1995–2019 | CCI-Lakes | ESA | Daily to weekly | 100 m |
| In-situ weather data | 1990-date | MET1 | FEM | Hourly | Single point |
| 2012-date | MET2 | ARPA-Lombardia | Hourly | Single point | |
| Global model weather data | 1950-date | ERA5 | ECMWF | Hourly | 0.1° (~11 km) |
| Regional model weather data | 2004–2018 | WRF | [35,59] | Hourly | 2 km |
| Simulated instantaneous evaporation maps | 2004–2018 | Delft3D | [35] | Daily | 100–400 m |
| Instantaneous Evaporation | ||||||
|---|---|---|---|---|---|---|
| Meteorology Source | RMSD | BIAS | Corr | NSE | Mean ± Std LakeVap | Mean ± Std Delft3D |
| (mm/h) | (mm/h) | (-) | (-) | (mm/h) | (mm/h) | |
| WRF | 0.04 | 0.006 | 0.92 | 0.834 | 0.129 ± 0.081 | 0.128 ± 0.098 |
| MET1 | 0.087 | −0.02 | 0.517 | 0.218 | 0.101 ± 0.058 | |
| MET2 * | 0.081 | 0.001 | 0.614 | 0.308 | 0.128 ± 0.0858 | |
| ERA5 | 0.091 | −0.045 | 0.606 | 0.129 | 0.078 ± 0.044 | |
| Lake Surface Water Temperature | ||||||
| LSWT source | RMSD | BIAS | Corr | NSE | Mean ± Std CCI-Lakes | Mean ± Std Delft3D |
| (°C) | (°C) | (-) | (-) | (°C) | (°C) | |
| CCI-Lakes database | 1.745 | 0.536 | 0.958 | 0.906 | 14.81 ± 5.75 | 14.27 ± 5.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matta, E.; Amadori, M.; Free, G.; Giardino, C.; Bresciani, M. A Satellite-Based Tool for Mapping Evaporation in Inland Water Bodies: Formulation, Application, and Operational Aspects. Remote Sens. 2022, 14, 2636. https://doi.org/10.3390/rs14112636
Matta E, Amadori M, Free G, Giardino C, Bresciani M. A Satellite-Based Tool for Mapping Evaporation in Inland Water Bodies: Formulation, Application, and Operational Aspects. Remote Sensing. 2022; 14(11):2636. https://doi.org/10.3390/rs14112636
Chicago/Turabian StyleMatta, Erica, Marina Amadori, Gary Free, Claudia Giardino, and Mariano Bresciani. 2022. "A Satellite-Based Tool for Mapping Evaporation in Inland Water Bodies: Formulation, Application, and Operational Aspects" Remote Sensing 14, no. 11: 2636. https://doi.org/10.3390/rs14112636