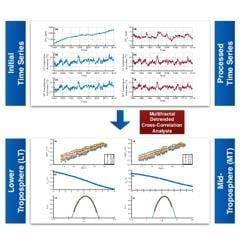
Multifractal Detrended Cross-Correlation Analysis of Global Methane and Temperature
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Methodology
2.2.1. Multifractal Detrended Fluctuation Analysis (MF-DFA)
2.2.2. Multifractal Detrended Cross-Correlation Analysis (MF-DCCA)
3. Results and Discussion
3.1. MF-DFA Results
3.2. MF-DCCA Results
3.2.1. Lower Troposphere
3.2.2. Mid-Troposphere
3.2.3. Origins of Multifractality
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Santer, B.D.; Solomon, S.; Wentz, F.J.; Fu, Q.; Po-Chedley, S.; Mears, C.; Painter, J.F.; Bonfils, C. Tropospheric Warming over the Past Two Decades. Sci. Rep. 2017, 7, 2336. [Google Scholar] [CrossRef]
- Hawkins, E.; Ortega, P.; Suckling, E.; Schurer, A.; Hegerl, G.; Jones, P.; Joshi, M.; Osborn, T.J.; Masson-Delmotte, V.; Mignot, J.; et al. Estimating Changes in Global Temperature since the Preindustrial Period. Bull. Am. Meteorol. Soc. 2017, 98, 1841–1856. [Google Scholar] [CrossRef]
- Thompson, D.W.J.; Seidel, D.J.; Randel, W.J.; Zou, C.-Z.; Butler, A.H.; Mears, C.; Osso, A.; Long, C.; Lin, R. The mystery of recent stratospheric temperature trends. Nature 2012, 491, 692–697. [Google Scholar] [CrossRef] [PubMed]
- Tzanis, C.G.; Koutsogiannis, I.; Philippopoulos, K.; Deligiorgi, D. Recent climate trends over Greece. Atmos. Res. 2019, 230, 104623. [Google Scholar] [CrossRef]
- Randel, W.J.; Polvani, L.; Wu, F.; Kinnison, D.E.; Zou, C.-Z.; Mears, C. Troposphere-Stratosphere Temperature Trends Derived From Satellite Data Compared With Ensemble Simulations From WACCM. J. Geophys. Res. Atmos. 2017, 122, 9651–9667. [Google Scholar] [CrossRef]
- Santer, B.D.; Fyfe, J.C.; Pallotta, G.; Flato, G.M.; Meehl, G.A.; England, M.H.; Hawkins, E.; Mann, M.E.; Painter, J.F.; Bonfils, C.; et al. Causes of differences in model and satellite tropospheric warming rates. Nat. Geosci. 2017, 10, 478–485. [Google Scholar] [CrossRef]
- Santer, B.D.; Solomon, S.; Pallotta, G.; Mears, C.; Po-Chedley, S.; Fu, Q.; Wentz, F.; Zou, C.-Z.; Painter, J.; Cvijanovic, I.; et al. Comparing Tropospheric Warming in Climate Models and Satellite Data. J. Clim. 2017, 30, 373–392. [Google Scholar] [CrossRef]
- National Research Council. Climate Data Records from Environmental Satellites: Interim Report; The National Academies Press: Washington, DC, USA, 2004. [Google Scholar]
- Christy, J.R.; Spencer, R.W.; Braswell, W.D.; Junod, R. Examination of space-based bulk atmospheric temperatures used in climate research. Int. J. Remote Sens. 2018, 39, 3580–3607. [Google Scholar] [CrossRef] [Green Version]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; 1535p. [Google Scholar]
- Etminan, M.; Myhre, G.; Highwood, E.J.; Shine, K.P. Radiative forcing of carbon dioxide, methane, and nitrous oxide: A significant revision of the methane radiative forcing. Geophys. Res. Lett. 2016, 43, 12614–12623. [Google Scholar] [CrossRef]
- Allen, M.R.; Shine, K.P.; Fuglestvedt, J.S.; Millar, R.J.; Cain, M.; Frame, D.J.; Macey, A.H. A solution to the misrepresentations of CO2-equivalent emissions of short-lived climate pollutants under ambitious mitigation. npj Clim. Atmos. Sci. 2018, 1, 16. [Google Scholar] [CrossRef]
- Azar, C.; Johansson, D.J.A. On the relationship between metrics to compare greenhouse gases; the case of IGTP, GWP and SGTP. Earth Syst. Dyn. 2012, 3, 139–147. [Google Scholar] [CrossRef] [Green Version]
- Myhre, G.; Shindell, D.; Bréon, F.-M.; Collins, W.D.; Fuglestvedt, J.; Huang, J.; Koch, D.; Lamarque, J.-F.; Lee, D.; Mendoza, B.; et al. Anthropogenic and Natural Radiative Forcing. In Climate Change 2013—The Physical Science Basis; Stocker, T., Ed.; Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; pp. 659–740. [Google Scholar]
- Prather, M.J.; Holmes, C.D.; Hsu, J. Reactive greenhouse gas scenarios: Systematic exploration of uncertainties and the role of atmospheric chemistry. Geophys. Res. Lett. 2012, 39, L09803. [Google Scholar] [CrossRef] [Green Version]
- Fiore, A.M.; Dentener, F.J.; Wild, O.; Cuvelier, C.; Schultz, M.G.; Hess, P.; Textor, C.; Schulz, M.; Doherty, R.M.; Horowitz, L.W.; et al. Multimodel estimates of intercontinental source-receptor relationships for ozone pollution. J. Geophys. Res. 2009, 114, D04301. [Google Scholar] [CrossRef]
- Voulgarakis, A.; Naik, V.; Lamarque, J.-F.; Shindell, D.T.; Young, P.J.; Prather, M.J.; Wild, O.; Field, R.D.; Bergmann, D.; Cameron-Smith, P.; et al. Analysis of present day and future OH and methane lifetime in the ACCMIP simulations. Atmos. Chem. Phys. 2013, 13, 2563–2587. [Google Scholar] [CrossRef] [Green Version]
- Kirschke, S.; Bousquet, P.; Ciais, P.; Saunois, M.; Canadell, J.G.; Dlugokencky, E.J.; Bergamaschi, P.; Bergmann, D.; Blake, D.R.; Bruhwiler, L.; et al. Three decades of global methane sources and sinks. Nat. Geosci. 2013, 6, 813–823. [Google Scholar] [CrossRef]
- Saunois, M.; Bousquet, P.; Poulter, B.; Peregon, A.; Ciais, P.; Canadell, J.G.; Dlugokencky, E.J.; Etiope, G.; Bastviken, D.; Houweling, S.; et al. The global methane budget 2000–2012. Earth Syst. Sci. Data 2016, 8, 697–751. [Google Scholar] [CrossRef] [Green Version]
- Holmes, C.D.; Prather, M.J.; Søvde, O.A.; Myhre, G. Future methane, hydroxyl, and their uncertainties: Key climate and emission parameters for future predictions. Atmos. Chem. Phys. 2013, 13, 285–302. [Google Scholar] [CrossRef] [Green Version]
- Frank, F.; Jöckel, P.; Gromov, S.; Dameris, M. Investigating the yield of H2O and H2 from methane oxidation in the stratosphere. Atmos. Chem. Phys. 2018, 13, 9955–9973. [Google Scholar] [CrossRef] [Green Version]
- Dlugokencky, E.J.; Nisbet, E.G.; Fisher, R.; Lowry, D. Global atmospheric methane: Budget, changes and dangers. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2011, 369, 2058–2072. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, D.L. Global Physical Climatology, 2nd ed.; Elsevier: Waltham, MA, USA, 2016; ISBN 9780123285317. [Google Scholar]
- Turner, A.J.; Frankenberg, C.; Wennberg, P.O.; Jacob, D.J. Ambiguity in the causes for decadal trends in atmospheric methane and hydroxyl. Proc. Natl. Acad. Sci. USA 2017, 114, 5367–5372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bergamaschi, P.; Houweling, S.; Segers, A.; Krol, M.; Frankenberg, C.; Scheepmaker, R.A.; Dlugokencky, E.; Wofsy, S.C.; Kort, E.A.; Sweeney, C.; et al. Atmospheric CH 4 in the first decade of the 21st century: Inverse modeling analysis using SCIAMACHY satellite retrievals and NOAA surface measurements. J. Geophys. Res. Atmos. 2013, 118, 7350–7369. [Google Scholar] [CrossRef] [Green Version]
- Bousquet, P.; Ringeval, B.; Pison, I.; Dlugokencky, E.J.; Brunke, E.-G.; Carouge, C.; Chevallier, F.; Fortems-Cheiney, A.; Frankenberg, C.; Hauglustaine, D.A.; et al. Source attribution of the changes in atmospheric methane for 2006–2008. Atmos. Chem. Phys. 2011, 11, 3689–3700. [Google Scholar] [CrossRef] [Green Version]
- Dlugokencky, E.J.; Bruhwiler, L.; White, J.W.C.; Emmons, L.K.; Novelli, P.C.; Montzka, S.A.; Masarie, K.A.; Lang, P.M.; Crotwell, A.M.; Miller, J.B.; et al. Observational constraints on recent increases in the atmospheric CH 4 burden. Geophys. Res. Lett. 2009, 36, L18803. [Google Scholar] [CrossRef] [Green Version]
- Nisbet, E.G.; Dlugokencky, E.J.; Bousquet, P. Methane on the Rise--Again. Science 2014, 343, 493–495. [Google Scholar] [CrossRef] [Green Version]
- Nisbet, E.G.; Dlugokencky, E.J.; Manning, M.R.; Lowry, D.; Fisher, R.E.; France, J.L.; Michel, S.E.; Miller, J.B.; White, J.W.C.; Vaughn, B.; et al. Rising atmospheric methane: 2007-2014 growth and isotopic shift. Glob. Biogeochem. Cycles 2016, 30, 1356–1370. [Google Scholar] [CrossRef] [Green Version]
- Rigby, M.; Prinn, R.G.; Fraser, P.J.; Simmonds, P.G.; Langenfelds, R.L.; Huang, J.; Cunnold, D.M.; Steele, L.P.; Krummel, P.B.; Weiss, R.F.; et al. Renewed growth of atmospheric methane. Geophys. Res. Lett. 2008, 35, L22805. [Google Scholar] [CrossRef] [Green Version]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef] [Green Version]
- Sadegh Movahed, M.; Hermanis, E. Fractal analysis of river flow fluctuations. Phys. A 2008, 387, 915–932. [Google Scholar] [CrossRef] [Green Version]
- Movahed, M.S.; Jafari, G.R.; Ghasemi, F.; Rahvar, S.; Tabar, M.R.R. Multifractal detrended fluctuation analysis of sunspot time series. J. Stat. Mech. Theory Exp. 2006, 2006, P02003. [Google Scholar] [CrossRef] [Green Version]
- Baranowski, P.; Krzyszczak, J.; Slawinski, C.; Hoffmann, H.; Kozyra, J.; Nieróbca, A.; Siwek, K.; Gluza, A. Multifractal analysis of meteorological time series to assess climate impacts. Clim. Res. 2015, 65, 39–52. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Zhang, Q.; Singh, V.P. Fractal-based evaluation of the effect of water reservoirs on hydrological processes: The dams in the Yangtze River as a case study. Stoch. Environ. Res. Risk Assess. 2014, 28, 263–279. [Google Scholar] [CrossRef]
- Du, H.; Wu, Z.; Zong, S.; Meng, X.; Wang, L. Assessing the characteristics of extreme precipitation over northeast China using the multifractal detrended fluctuation analysis. J. Geophys. Res. Atmos. 2013, 118, 6165–6174. [Google Scholar] [CrossRef]
- Xue, Y.; Pan, W.; Lu, W.-Z.; He, H.-D. Multifractal nature of particulate matters (PMs) in Hong Kong urban air. Sci. Total Environ. 2015, 532, 744–751. [Google Scholar] [CrossRef] [PubMed]
- Kalamaras, N.; Philippopoulos, K.; Deligiorgi, D.; Tzanis, C.G.; Karvounis, G. Multifractal scaling properties of daily air temperature time series. Chaos Solitons Fractals 2017, 98, 38–43. [Google Scholar] [CrossRef]
- Kalamaras, N.; Tzanis, C.G.; Deligiorgi, D.; Philippopoulos, K.; Koutsogiannis, I. Distribution of air temperature multifractal characteristics over Greece. Atmosphere 2019, 10, 45. [Google Scholar] [CrossRef] [Green Version]
- Philippopoulos, K.; Kalamaras, N.; Tzanis, C.G.; Deligiorgi, D.; Koutsogiannis, I. Multifractal Detrended Fluctuation Analysis of temperature reanalysis data over Greece. Atmosphere 2019, 10, 336. [Google Scholar] [CrossRef] [Green Version]
- Podobnik, B.; Stanley, H.E. Detrended Cross-Correlation Analysis: A New Method for Analyzing Two Nonstationary Time Series. Phys. Rev. Lett. 2008, 100, 084102. [Google Scholar] [CrossRef] [Green Version]
- Gvozdanovic, I.; Podobnik, B.; Wang, D.; Eugene Stanley, H. 1/f behavior in cross-correlations between absolute returns in a US market. Physica A 2012, 391, 2860–2866. [Google Scholar] [CrossRef]
- Horvatic, D.; Stanley, H.E.; Podobnik, B. Detrended cross-correlation analysis for non-stationary time series with periodic trends. Europhys. Lett. 2011, 94, 18007. [Google Scholar] [CrossRef] [Green Version]
- Marinho, E.B.S.; Sousa, A.M.Y.R.; Andrade, R.F.S. Using Detrended Cross-Correlation Analysis in geophysical data. Phys. A 2013, 392, 2195–2201. [Google Scholar] [CrossRef] [Green Version]
- Shen, C.; Li, C.; Si, Y. A detrended cross-correlation analysis of meteorological and API data in Nanjing, China. Phys. A 2015, 419, 417–428. [Google Scholar] [CrossRef]
- Liao, W.; Wang, X.; Fan, Q.; Zhou, S.; Chang, M.; Wang, Z.; Wang, Y.; Tu, Q. Long-term atmospheric visibility, sunshine duration and precipitation trends in South China. Atmos. Environ. 2015, 107, 204–216. [Google Scholar] [CrossRef]
- Zhou, W.-X. Multifractal detrended cross-correlation analysis for two nonstationary signals. Phys. Rev. E 2008, 77, 066211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, C.; Ni, Z.; Ni, L. Multifractal detrended cross-correlation analysis between PM2.5 and meteorological factors. Phys. A 2015, 438, 114–123. [Google Scholar] [CrossRef]
- Hajian, S.; Movahed, M.S. Multifractal Detrended Cross-Correlation Analysis of sunspot numbers and river flow fluctuations. Phys. A 2010, 389, 4942–4957. [Google Scholar] [CrossRef] [Green Version]
- Kar, A.; Chatterjee, S.; Ghosh, D. Multifractal detrended cross-correlation analysis of Land-surface temperature anomalies and Soil radon concentration. Phys. A 2019, 521, 236–247. [Google Scholar] [CrossRef]
- Spencer, R.W.; Christy, J.R.; Braswell, W.D. UAH Version 6 global satellite temperature products: Methodology and results. Asia-Pac. J. Atmos. Sci. 2017, 53, 121–130. [Google Scholar] [CrossRef]
- Dlugokencky, E.J.; Steele, L.P.; Lang, P.M.; Masarie, K.A. The growth rate and distribution of atmospheric methane. J. Geophys. Res. 1994, 99, 17021. [Google Scholar] [CrossRef]
- Masarie, K.A.; Tans, P.P. Extension and integration of atmospheric carbon dioxide data into a globally consistent measurement record. J. Geophys. Res. 1995, 100, 11593. [Google Scholar] [CrossRef] [Green Version]
- Ed Dlugokencky, NOAA/ESRL. Available online: https://www.esrl.noaa.gov/gmd/ccgg/trends_ch4/ (accessed on 13 November 2019).
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series; The MIT Press: Cambridge, MA, USA, 1964. [Google Scholar]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Order parameter fluctuations of seismicity in natural time before and after mainshocks. EPL 2010, 91, 59001. [Google Scholar] [CrossRef]
- Skordas, E.S.; Sarlis, N.V.; Varotsos, P.A. Effect of significant data loss on identifying electric signals that precede rupture estimated by detrended fluctuation analysis in natural time. Chaos 2010, 20, 033111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varotsos, C.A.; Tzanis, C. A new tool for the study of the ozone hole dynamics over Antarctica. Atmos. Environ. 2012, 47, 428–434. [Google Scholar] [CrossRef]
- Chattopadhyay, G.; Chattopadhyay, S. Study on statistical aspects of monthly sunspot number time series and its long-range correlation through detrended fluctuation analysis. Indian J. Phys. 2014, 88, 1135–1140. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Lovejoy, S.; Sarlis, N.V.; Tzanis, C.G.; Efstathiou, M.N. On the scaling of the solar incident flux. Atmos. Chem. Phys. 2015, 15, 7301–7306. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, Y.; Thurner, S.; Ehrenberger, K. Multifractal spectra as a measure of complexity in human posture. Fractals 2002, 10, 103–116. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Efstathiou, M.N. Has global warming already arrived? J. Atmos. Sol.-Terr. Phys. 2019, 182, 31–38. [Google Scholar] [CrossRef]
- Mali, P. Multifractal characterization of global temperature anomalies. Theor. Appl. Climatol. 2015, 121, 641–648. [Google Scholar] [CrossRef]
- Tzanis, C. On the relationship between total ozone and temperature in the troposphere and the lower stratosphere. Int. J. Remote Sens. 2009, 30, 6075–6084. [Google Scholar] [CrossRef]
- Amanollahi, J.; Tzanis, C.; Ramli, M.F.; Abdullah, A.M. Urban heat evolution in a tropical area utilizing Landsat imagery. Atmos. Res. 2016, 167, 175–182. [Google Scholar] [CrossRef]
- Varotsos, C.A.; Melnikova, I.N.; Cracknell, A.P.; Tzanis, C.; Vasilyev, A.V. New spectral functions of the near-ground albedo derived from aircraft diffraction spectrometer observations. Atmos. Chem. Phys. 2014, 14, 6953–6965. [Google Scholar] [CrossRef] [Green Version]
- Tzanis, C.; Varotsos, C.A. Tropospheric aerosol forcing of climate: A case study for the greater area of Greece. Int. J. Remote Sens. 2008, 29, 2507–2517. [Google Scholar] [CrossRef]
- Lelieveld, J.; Crutzen, P.J. Indirect chemical effects of methane on climate warming. Nature 1992, 355, 339–342. [Google Scholar] [CrossRef]
- Cui, M.; Ma, A.; Qi, H.; Zhuang, X.; Zhuang, G.; Zhao, G. Warmer temperature accelerates methane emissions from the Zoige wetland on the Tibetan Plateau without changing methanogenic community composition. Sci. Rep. 2015, 5, 11616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dean, J.F.; Middelburg, J.J.; Röckmann, T.; Aerts, R.; Blauw, L.G.; Egger, M.; Jetten, M.S.M.; de Jong, A.E.E.; Meisel, O.H.; Rasigraf, O.; et al. Methane Feedbacks to the Global Climate System in a Warmer World. Rev. Geophys. 2018, 56, 207–250. [Google Scholar] [CrossRef]





| Parameter | CH4 | Temperature Anomalies (LT) | Temperature Anomalies (MT) | CC (LT) | CC (MT) |
|---|---|---|---|---|---|
| α0 | 1.714 | 1.387 | 1.441 | 1.558 | 1.582 |
| w | 0.790 | 1.108 | 1.128 | 0.887 | 0.757 |
| Parameter | CH4 | Temperature Anomalies (LT) | Temperature Anomalies (MT) | CC (LT) | CC (MT) |
|---|---|---|---|---|---|
| α0 | 0.508 | 0.527 | 0.508 | 0.524 | 0.500 |
| w | 0.288 | 0.265 | 0.280 | 0.229 | 0.317 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzanis, C.G.; Koutsogiannis, I.; Philippopoulos, K.; Kalamaras, N. Multifractal Detrended Cross-Correlation Analysis of Global Methane and Temperature. Remote Sens. 2020, 12, 557. https://doi.org/10.3390/rs12030557
Tzanis CG, Koutsogiannis I, Philippopoulos K, Kalamaras N. Multifractal Detrended Cross-Correlation Analysis of Global Methane and Temperature. Remote Sensing. 2020; 12(3):557. https://doi.org/10.3390/rs12030557
Chicago/Turabian StyleTzanis, Chris G., Ioannis Koutsogiannis, Kostas Philippopoulos, and Nikolaos Kalamaras. 2020. "Multifractal Detrended Cross-Correlation Analysis of Global Methane and Temperature" Remote Sensing 12, no. 3: 557. https://doi.org/10.3390/rs12030557