Pharma 4.0-Artificially Intelligent Digital Twins for Solidified Nanosuspensions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Process Design
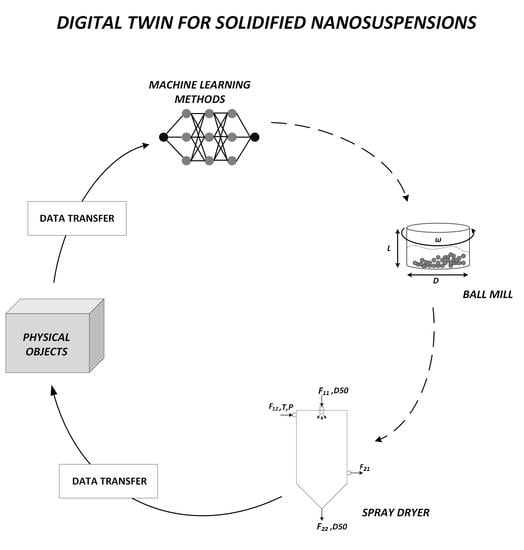
2.2. Experimental Study and Digital Twin Thread Structuring
2.3. Integration of Artificial Neural Networks for Parameter Tuning
3. Results
3.1. Material Critical Quality Attributes and the Material System’s Interfacial Gibbs Energy Assesment
3.2. Parameter Fitting
3.3. Sensitivity Analysis
3.3.1. Wet Milling
3.3.2. Spray Drying
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in Manufacturing: A Categorical Literature Review and Classification. IFAC-PapersOnLine 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- Udugama, I.A.; Lopez, P.C.; Gargalo, C.L.; Li, X.; Bayer, C.; Gernaey, K.V. Digital Twin in Biomanufacturing: Challenges and Opportunities towards Its Implementation. Syst. Microbiol. Biomanuf. 2021, 1, 257–274. [Google Scholar] [CrossRef]
- Ouranidis, A.; Davidopoulou, C.; Tashi, R.K.; Kachrimanis, K. Pharma 4.0 Continuous MRNA Drug Products Manufacturing. Pharmaceutics 2021, 13, 1371. [Google Scholar] [CrossRef] [PubMed]
- Sutariya, V.B.; Groshev, A.; Pathak, Y.V. Artificial Neural Networks in Pharmaceutical Research, Drug Delivery and Pharmacy Curriculum. In Proceedings of the 29th Southern Biomedical Engineering Conference 2013, Miami, FL, USA, 3–5 May 2013; pp. 91–92. [Google Scholar] [CrossRef]
- Mandlik, V.; Bejugam, P.R.; Singh, S. Application of Artificial Neural Networks in Modern Drug Discovery; Elsevier Inc.: Amsterdam, The Netherlands, 2016; ISBN 9780128015599. [Google Scholar]
- Wang, S.; Di, J.; Wang, D.; Dai, X.; Hua, Y.; Gao, X.; Zheng, A.; Gao, J. State-of-the-Art Review of Artificial Neural Networks to Predict, Characterize and Optimize Pharmaceutical Formulation. Pharmaceutics 2022, 14, 183. [Google Scholar] [CrossRef]
- Ouranidis, A.; Davidopoulou, C.; Kachrimanis, K. Integrating Elastic Tensor and Pc-Saft Modeling with Systems-Based Pharma 4.0 Simulation, to Predict Process Operations and Product Specifications of Ternary Nanocrystalline Suspensions. Pharmaceutics 2021, 13, 1771. [Google Scholar] [CrossRef]
- Brynjarsdóttir, J.; Ohagan, A. Learning about Physical Parameters: The Importance of Model Discrepancy. Inverse Probl. 2014, 30, 114007. [Google Scholar] [CrossRef]
- Ge, K.; Ji, Y.; Lu, X. A Novel Interfacial Thermodynamic Model for Predicting Solubility of Nanoparticles Coated by Stabilizers. Chin. J. Chem. Eng. 2021, 31, 103–112. [Google Scholar] [CrossRef]
- Ferreira-Pinto, L.; De Araujo, P.C.C.; Aranda Saldaña, M.D.; Arce, P.F.; Cardozo-Filho, L. Experimental Data and Thermodynamics Modeling (PC-SAFT EoS) of the {CO 2 + Acetone + Pluronic F-127} System at High Pressures. J. Chem. Eng. Data 2019, 64, 2186–2192. [Google Scholar] [CrossRef]
- Bodratti, A.M.; Alexandridis, P. Formulation of Poloxamers for Drug Delivery. J. Funct. Biomater. 2018, 9, 11. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Zhang, Z.; Gao, R.; Li, H.; Dong, Z.; Wang, Q.; Zhou, Q.; Wang, Y. Physiologically Stable F127-GO Supramolecular Hydrogel with Sustained Drug Release Characteristic for Chemotherapy and Photothermal Therapy. RSC Adv. 2018, 8, 1693–1699. [Google Scholar] [CrossRef] [Green Version]
- Szafraniec, J.; Antosik, A.; Knapik-Kowalczuk, J.; Chmiel, K.; Kurek, M.; Gawlak, K.; Odrobińska, J.; Paluch, M.; Jachowicz, R. The Self-Assembly Phenomenon of Poloxamers and Its Effect on the Dissolution of a Poorly Soluble Drug from Solid Dispersions Obtained by Solvent Methods. Pharmaceutics 2019, 11, 130. [Google Scholar] [CrossRef] [Green Version]
- Guth, F.; Staal, B.; Jackson, T. Kolliphor ® P 188 Bio: A New Era in Shear Protection; BASF Corporation: Florham Park, NJ, USA, 2017; pp. 1–4. [Google Scholar]
- De Vegt, O.; Vromans, H.; Faassen, F.; Van Der Voort Maarschalk, K. Milling of Organic Solids in a Jet Mill. Part 2: Checking the Validity of the Predicted Rate of Breakage Function. Part. Part. Syst. Charact. 2006, 22, 261–267. [Google Scholar] [CrossRef]
- Austin, L.; Shoji, K.; Bhatia, V.; Jindal, V.; Savage, K.; Klimpel, R. Some Results on the Description of Size Reduction as a Rate Process in Various Mills. Ind. Eng. Chem. Process Des. Dev. 1976, 15, 187–196. [Google Scholar] [CrossRef]
- Kapur, P.C. Self-Preserving Size Spectra of Comminuted Particles. Chem. Eng. Sci. 1972, 27, 425–431. [Google Scholar] [CrossRef]
- Oakley, D.E. Spray Dryer Modeling in Theory and Practice. Dry. Technol. 2004, 22, 1371–1402. [Google Scholar] [CrossRef]
- Pavlidou, M.; Κyriakos, K. Influence of Formulation Factors on Production of Microcomposite Particles for Inhalation; Aristotle University of Thessaloniki: Thessaloniki, Greece, 2018. [Google Scholar] [CrossRef]
- Brenan, B.K.E.; Engquist, B.E. Backward Differentiation Approximations of Nonlinear Differential/Algebraic Systems; American Mathematical Society: Providence, RI, USA, 1998; Volume 51, pp. 659–676. Available online: Https://www.Jstor.Org/Stable/2008768 (accessed on 8 September 2022).
- Thanuja, B.; Kanagam, C.; Sreedevi, S. Studies on Intermolecular Interaction on Binary Mixtures of Methyl Orange-Water System: Excess Molar Functions of Ultrasonic Parameters at Different Concentrations and at Different Temperatures. Ultrason. Sonochem. 2011, 18, 1274–1278. [Google Scholar] [CrossRef]
- Kojima, T.; Karashima, M.; Yamamoto, K.; Ikeda, Y. Combination of NMR Methods to Reveal the Interfacial Structure of a Pharmaceutical Nanocrystal and Nanococrystal in the Suspended State. Mol. Pharm. 2018, 15, 3901–3908. [Google Scholar] [CrossRef]
- Shnoudeh, A.J.; Hamad, I.; Abdo, R.W.; Qadumii, L.; Jaber, A.Y.; Surchi, H.S.; Alkelany, S.Z. Synthesis, Characterization, and Applications of Metal Nanoparticles; Elsevier Inc.: Amsterdam, The Netherlands, 2019; ISBN 9780128144282. [Google Scholar]
- Rolnick, D.; Veit, A.; Belongie, S.; Shavit, N. Deep Learning Is Robust to Massive Label Noise. arXiv 2017, arXiv:1705.10694. [Google Scholar]
- News, T.; News, T. Improving Pulp M Ill Ill Operation Operation With Digital Twin Twin Technology. Tech News 2018, 2, 49–50. [Google Scholar]
- Ouranidis, A.; Gkampelis, N.; Markopoulou, C.; Nikolakakis, I.; Kachrimanis, K. Development of a Nanocrystal Formulation of a Low Melting Point Api Following a Quality by Design Approach. Processes 2021, 9, 954. [Google Scholar] [CrossRef]
- Singh, A.; Van den Mooter, G. Spray Drying Formulation of Amorphous Solid Dispersions. Adv. Drug Deliv. Rev. 2016, 100, 27–50. [Google Scholar] [CrossRef] [PubMed]
- Scardi, M. Artificial Neural Networks as Empirical Models for Estimating Phytoplankton Production. Mar. Ecol. Prog. Ser. 1996, 139, 289–299. [Google Scholar] [CrossRef] [Green Version]
- Ouranidis, A.; Tsiaxerli, A.; Vardaka, E.; Markopoulou, C.K.; Zacharis, C.K.; Nicolaou, I.; Hatzichristou, D.; Haidich, A.-B.; Kostomitsopoulos, N.; Kachrimanis, K. Sildenafil 4.0—Integrated Synthetic Chemistry, Formulation and Analytical Strategies Effecting Immense Therapeutic and Societal Impact in the Fourth Industrial Era. Pharmaceuticals 2021, 14, 365. [Google Scholar] [CrossRef] [PubMed]










| Group | mseg (−) | σi (A) | ui/k (K) | Source |
|---|---|---|---|---|
| EO | 0.052 ΜWtotal | 2.89 | 206.74 | [10,11,12,13,14] |
| PO | 0.037 MWtotal | 3.34 | 192.72 |
| Time (s) | Experiment 1 D50 (μm) | Experiment 2 D50 (μm) | Experiment 3 D50 (μm) |
|---|---|---|---|
| 360 | 1.39 | 1.31 | 1.37 |
| 720 | 0.874 | 0.792 | 0.846 |
| 1440 | 0.784 | 0.742 | 0.783 |
| 2160 | 0.522 | 0.501 | 0.520 |
| 2880 | 0.467 | 0.434 | 0.436 |
| 3600 | 0.305 | 0.297 | 0.301 |
| MODEL | PARAMETER | TYPE | VALUE | UNIT |
|---|---|---|---|---|
| Water quantity | input | 9 | mL | |
| API content | input | 0.5 | g | |
| Stabilizer content | input | 0.25 | g | |
| Mannitol content | input | 1 | g | |
| Wet mill | Initial particle size (D50) | input | 1.5 | μm |
| Grinding time | input | 1 | h | |
| Rotor speed | input | 600 | rpm | |
| Rotor diameter | input | 40 | mm | |
| Equipment volume | input | 48 | mL | |
| D50(t) | output | - | - | |
| Air temperature | input | 110 | °C | |
| Air flow | input | 800 | L h−1 | |
| Spray dryer | Air pressure | input | 5 | bar |
| Drying chamber volume | input | 5 | L | |
| Drying time | input | 1 | h | |
| Final product size (D50) | output | 10 | μm |
| Stabilizer | Density (kg m−3) | Z-Potential | |
|---|---|---|---|
| HPC-SL | 0.0019 | 1320 | −11.7 |
| Poloxamer-407 | 0.0039 | 954 | −13.7 |
| Poloxame-188 | 0.0056 | 951 | −17.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davidopoulou, C.; Ouranidis, A. Pharma 4.0-Artificially Intelligent Digital Twins for Solidified Nanosuspensions. Pharmaceutics 2022, 14, 2113. https://doi.org/10.3390/pharmaceutics14102113
Davidopoulou C, Ouranidis A. Pharma 4.0-Artificially Intelligent Digital Twins for Solidified Nanosuspensions. Pharmaceutics. 2022; 14(10):2113. https://doi.org/10.3390/pharmaceutics14102113
Chicago/Turabian StyleDavidopoulou, Christina, and Andreas Ouranidis. 2022. "Pharma 4.0-Artificially Intelligent Digital Twins for Solidified Nanosuspensions" Pharmaceutics 14, no. 10: 2113. https://doi.org/10.3390/pharmaceutics14102113