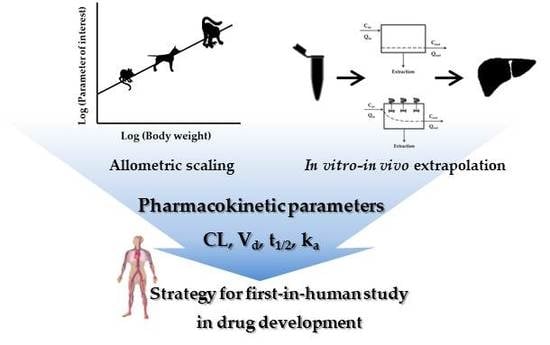
Interpretation of Non-Clinical Data for Prediction of Human Pharmacokinetic Parameters: In Vitro-In Vivo Extrapolation and Allometric Scaling
Abstract
:1. Introduction
2. Theoretical Background for the Prediction of Clearance
2.1. Physiological Clearance Concept
2.1.1. Organ Clearance
- The first situation is when the clearance capacity (i.e., CLint) exceeds the Q (CLint >> Q). In this situation, Equation (12) collapses and transforms to Equation (13).
- The second situation is when Cout is a small fraction of Cin (i.e., when Kp is high, or ER is low). [34]. In this case, Equation (12) collapses in the following equation:
2.1.2. Consideration of Enzyme Kinetics
2.1.3. Hepatic Clearance Model
Well-Stirred Model
Parallel-Tube Model
Distributed Model and Dispersion Model
3. Prediction of Human Clearance Using IVIVE Method
3.1. IVIVE
3.1.1. Empirical IVIVE Model
3.1.2. Correction Factor of IVIVE Model
Protein Binding Factor
Animal Scaling Factor
3.1.3. Inter-Individual Variability (IIV) in the IVIVE Method
Microsomal Protein Content and CYP Abundance
Microsomal Protein per Gram of Liver (MPPGL)
Inter-System Extrapolation Factor (ISEF)
3.1.4. Additional Correction Factors
FI
Effective Fraction Unbound in Plasma
3.1.5. Physiologically-Based IVIVE Model
4. Application of AS for the Prediction of Human PK Parameters
4.1. Concept of AS
4.2. Prediction of Clearance by AS
4.2.1. Two-Term Method
4.2.2. Rule of Exponent
4.2.3. One or Two Species Method
4.2.4. Liver Blood Flow
4.2.5. Incorporation of in Vitro Data
4.2.6. Protein Binding
4.2.7. QSAR Approach
4.2.8. Fraction Unbound Intercept Correction Method (FCIM)
4.2.9. Multiexponential Allometric Scaling (MA)
4.3. Prediction of Volume of Distribution by AS
4.3.1. Volume of Distribution in PKs
- Volume of distribution of central compartment (Vc).
- Volume of distribution at steady state (Vss)
- Volume of distribution by area (Varea), also known as Vβ
4.3.2. Prediction of Vd
4.3.3. Prediction of Elimination Half-Life by AS
5. Prediction of Absorption Related PK Parameters
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADME | absorption, distribution, metabolism, excretion |
| AS | allometric scaling |
| AUC0-inf | area under the concentration-time curve from zero to infinity |
| BDDCS | biopharmaceutics drug disposition classification system |
| BW | brain weight |
| CB | drug concentration in blood |
| CL | clearance |
| CLH | hepatic clearance |
| CLint | intrinsic clearance |
| CLint, H | hepatic intrinsic clearance |
| CLint,H, human | human hepatic intrinsic clearance |
| CLint,H, pred | predicted hepatic intrinsic clearance |
| CLint,in vitro | in vitro intrinsic clearance |
| CLint,met | intrinsic metabolic clearance |
| CLint,sec | intrinsic secretory clearance |
| CLmet | metabolic clearance |
| cLogP | partition coefficient |
| clogP | calculated logP |
| CLorg | organ clearance |
| CP | drug concentration in plasma |
| CR | concentration in VR |
| CRBC | drug concentration in red blood cells |
| Cu | unbound drug concentration at distribution equilibrium |
| DMPK | drug metabolism and pharmacokinetic |
| DN | dispersion number |
| ECM | extended clearance model |
| ER | extraction ratio |
| ERH | hepatic extraction ratio |
| ERH, obs | observed hepatic extraction ratio |
| ERH, pred | predicted hepatic extraction ratio |
| F | fraction of absorption |
| unbound fraction in the intracellular water of ionized compound | |
| unbound fraction in the intracellular water of neutral compound | |
| unbound fraction in the plasma of ionized compound | |
| unbound fraction in the plasma of neutral compound | |
| Fa | fraction of absorption |
| fb | unbound fraction in blood |
| FCIM | fraction unbound intercept correction method |
| FH | hepatic availability |
| FI | ionization factor |
| fnH | fractional contribution of hepatic elimination |
| fnmet | fractional contribution of metabolic elimination |
| fnsec | fractional contribution of biliary elimination |
| fp | unbound fraction in plasma |
| FPO | oral bioavailability |
| fu, mic | non-specific binding factor to microsomes |
| fu,liver | unbound fraction into the liver |
| Ha | number of hydrogen-bond acceptors |
| HBD | number of hydrogen-bond donor |
| Hct | hematocrit |
| HLM | human liver microsomes |
| IIV | inter-individual variability |
| ISEF | inter-system extrapolation factor |
| ISTD | internal standard |
| IVIVE | in vitro-in vivo extrapolation |
| IW | intracellular water |
| ka | absorption rate constant |
| ka,eq | equilibrium solution for ka |
| ki | the rate constant of intestinal transit |
| Km | Michaelis constant |
| L | length of perfusion segment |
| MA | multiexponential allometric scaling |
| MLBF | monkey liver blood flow |
| MLP | maximum life-span potential |
| MPPGL | microsomal protein per gram of liver |
| MPR | microsomal protein recovery |
| MRT | mean residence time |
| MW | molecular weight |
| NCA | non-compartmental analysis |
| Peff | effective permeability |
| PK | pharmacokinetic |
| PLR | plasma to whole liver concentration ratio |
| Pm | drug permeability across intestinal mucosa |
| PSA | polar surface area |
| PSbile | biliary clearance |
| PSefflux, total | apparent sinusoidal total efflux clearance from the intracellular side of hepatocytes back into blood |
| PSinf, act | sinusoidal efflux from hepatocytes back into blood |
| PSuptake,total | total apparent uptake clearance |
| QH | hepatic liver flow |
| QSAR | quantitative structure activity relationship |
| R | radius of human jejunum |
| RAF | relative activity factor |
| RB/P | blood to plasma ratio |
| RE/I | ratio of distributed albumin in the extravascular space to that in the intravascular space |
| Rfu | unbound fraction in plasma ratio between rats and humans |
| rhCYP | recombinant human CYP system |
| RN | efficiency number |
| ROE | rule of exponent |
| S | absorptive surface area |
| t1/2 | half-life |
| V | volume of distribution |
| Varea, Vβ | volume of distribution by area |
| Vc | volume of distribution of central compartment |
| VE | extracellular space volume minus the plasma volume |
| Vmax | maximal rate of the reaction |
| Vmet | metabolic rate |
| Vplasma | plasma volume |
| VR | physical volume into which the drug distributes minus the extracellular space |
| Vss | volume of distribution at steady state |
| W | body weight |
| ε2 | variance for each sinusoid in the whole liver |
References
- Prentis, R.A.; Lis, Y.; Walker, S.R. Pharmaceutical innovation by the seven UK-owned pharmaceutical companies (1964–1985). Br. J. Clin. Pharm. 1988, 25, 387–396. [Google Scholar] [CrossRef]
- Alavijeh, M.S.; Palmer, A.M. The pivotal role of drug metabolism and pharmacokinetics in the discovery and development of new medicines. Curr. Opin. Investig. Drugs 2004, 5, 755–763. [Google Scholar]
- Harrison, R.K. Phase II and phase III failures: 2013–2015. Nat. Rev. Drug Discov. 2016, 15, 817–818. [Google Scholar] [CrossRef] [PubMed]
- Kola, I.; Landis, J. Can the pharmaceutical industry reduce attrition rates? Nat. Rev. Drug Discov. 2004, 3, 711–715. [Google Scholar] [CrossRef]
- Wang, J.; Urban, L. The impact of early ADME profiling on drug discovery and development strategy. Drug Discov. World 2004, 5, 73–86. [Google Scholar]
- Mahmood, I.; Balian, J.D. The pharmacokinetic principles behind scaling from preclinical results to phase I protocols. Clin. Pharm. 1999, 36, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.H. Applications and limitations of interspecies scaling and in vitro extrapolation in pharmacokinetics. Drug Metab. Dispos. 1998, 26, 1202–1212. [Google Scholar]
- Riede, J.; Poller, B.; Umehara, K.; Huwyler, J.; Camenisch, G. New IVIVE method for the prediction of total human clearance and relative elimination pathway contributions from in vitro hepatocyte and microsome data. Eur. J. Pharm. Sci. 2016, 86, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, J.; Bao, X.; Honea, N.; Xie, Y.; Kim, S.; Sparreboom, A.; Sanai, N. Quantitative and Mechanistic Understanding of AZD1775 Penetration across Human Blood-Brain Barrier in Glioblastoma Patients Using an IVIVE-PBPK Modeling Approach. Clin. Cancer Res. Off. J. Am. Assoc. Cancer Res. 2017, 23, 7454–7466. [Google Scholar] [CrossRef] [PubMed]
- Zou, P.; Liu, X.; Wong, S.; Feng, M.R.; Liederer, B.M. Comparison of in vitro-in vivo extrapolation of biliary clearance using an empirical scaling factor versus transport-based scaling factors in sandwich-cultured rat hepatocytes. J. Pharm. Sci. 2013, 102, 2837–2850. [Google Scholar] [CrossRef] [PubMed]
- Knights, K.M.; Spencer, S.M.; Fallon, J.K.; Chau, N.; Smith, P.C.; Miners, J.O. Scaling factors for the in vitro-in vivo extrapolation (IV-IVE) of renal drug and xenobiotic glucuronidation clearance. Br. J. Clin. Pharm. 2016, 81, 1153–1164. [Google Scholar] [CrossRef]
- Scotcher, D.; Jones, C.; Posada, M.; Rostami-Hodjegan, A.; Galetin, A. Key to Opening Kidney for in Vitro-In Vivo Extrapolation Entrance in Health and Disease: Part I: In Vitro Systems and Physiological Data. AAPS J. 2016, 18, 1067–1081. [Google Scholar] [CrossRef] [PubMed]
- Scotcher, D.; Billington, S.; Brown, J.; Jones, C.R.; Brown, C.D.; Rostami-Hodjegan, A.; Galetin, A. Microsomal and Cytosolic Scaling Factors in Dog and Human Kidney Cortex and Application for In Vitro-In Vivo Extrapolation of Renal Metabolic Clearance. Drug Metab. Dispos. 2017, 45, 556–568. [Google Scholar] [CrossRef] [PubMed]
- Nishimuta, H.; Houston, J.B.; Galetin, A. Hepatic, intestinal, renal, and plasma hydrolysis of prodrugs in human, cynomolgus monkey, dog, and rat: Implications for in vitro-in vivo extrapolation of clearance of prodrugs. Drug Metab. Dispos. 2014, 42, 1522–1531. [Google Scholar] [CrossRef]
- Campbell, D.B. Can allometric interspecies scaling be used to predict human kinetics? Drug Inf. J. 1994, 28, 235–245. [Google Scholar] [CrossRef]
- Temerin, L.A. The ecological implications of body size. By R.H. Peters. New York: Cambridge University Press. 1983. xii + 329 pp., figures, tables, appendices, references, index. $29-95 (cloth). Am. J. Phys. Anthropol. 1985, 66, 340–342. [Google Scholar] [CrossRef]
- Boxenbaum, H.; Fertig, J.B. Scaling of antipyrine intrinsic clearance of unbound drug in 15 mammalian species. Eur. J. Drug Metab. Pharm. 1984, 9, 177–183. [Google Scholar] [CrossRef]
- Boxenbaum, H. Interspecies Scaling, Allometry, Physiological Time, and the Ground Plan of Pharmacokinetics. J. Pharm. Biopharm. 1982, 10, 201–227. [Google Scholar] [CrossRef]
- Boxenbaum, H. Interspecies variation in liver weight, hepatic blood flow, and antipyrine intrinsic clearance: Extrapolation of data to benzodiazepines and phenytoin. J. Pharm. Biopharm. 1981, 8, 165–176. [Google Scholar] [CrossRef]
- Dedrick, R.L. Animal scale-up. J. Pharm. Biopharm. 1973, 1, 435–461. [Google Scholar] [CrossRef]
- Adolph, E.F. Quantitative Relations in the Physiological Constitutions of Mammals. Science 1949, 109, 579–585. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Riviere, J.E. The application of allometric scaling principles to predict pharmacokinetic parameters across species. Expert Opin. Drug Metab. Toxicol. 2014, 10, 1241–1253. [Google Scholar] [CrossRef] [PubMed]
- Andrade, E.L.; Bento, A.F.; Cavalli, J.; Oliveira, S.K.; Schwanke, R.C.; Siqueira, J.M.; Freitas, C.S.; Marcon, R.; Calixto, J.B. Non-clinical studies in the process of new drug development—Part II: Good laboratory practice, metabolism, pharmacokinetics, safety and dose translation to clinical studies. Braz. J. Med. Biol. Res. 2016, 49, e5646. [Google Scholar] [CrossRef] [PubMed]
- Guidance for Industry: In Vitro Metabolism- and Transporter-Mediated Drug-Drug Interaction Studies; U.S. Department of Health and Human Services, Food and Drug Administration (FDA), Center for Drug Evaluation and Research (CDER): Rockville, MD, USA, 2017.
- Estimating the Maximum Safe Starting Dose in Initial Clinical Trials for Therapeutics in Adult Healthy Volunteers; U.S. Department of Health and Human Services, Food and Drug Administration (FDA), Center for Drug Evaluation and Research (CDER): Rockville, MD, USA, 2005.
- Ings, R.M. Interspecies scaling and comparisons in drug development and toxicokinetics. Xenobiotica 1990, 20, 1201–1231. [Google Scholar] [CrossRef] [PubMed]
- Zuegge, J.; Schneider, G.; Coassolo, P.; Lave, T. Prediction of hepatic metabolic clearance: Comparison and assessment of prediction models. Clin. Pharm. 2001, 40, 553–563. [Google Scholar] [CrossRef] [PubMed]
- Shargel, L.; Andrew, B.C.; Wu-Pong, S. Applied Biopharmaceutics & Pharmacokinetics, 7th ed.; Appleton & Lange Reviews/McGraw-Hill, Medical Pub. Division: New York, NY, USA, 2016. [Google Scholar]
- Pang, K.S.; Weiss, M.; Macheras, P. Advanced pharmacokinetic models based on organ clearance, circulatory, and fractal concepts. AAPS J. 2007, 9, E268–E283. [Google Scholar] [CrossRef] [PubMed]
- Mehvar, R. Interdependency of pharmacokinetic parameters: A chicken-and-egg problem? Not! J. Pharm. Pharm. Sci. 2006, 9, 113–118. [Google Scholar] [PubMed]
- Sirianni, G.L.; Pang, K.S. Organ Clearance Concepts: New Perspectives on Old Principles. J. Pharm. Biopharm. 1997, 25, 449–470. [Google Scholar] [CrossRef]
- Keiding, S.; Andreasen, P.B. Hepatic clearance measurements and pharmacokinetics. Pharmacology 1979, 19, 105–110. [Google Scholar] [CrossRef] [PubMed]
- Benet, L.Z.; Zia-Amirhosseini, P. Basic principles of pharmacokinetics. Toxicol. Pathol. 1995, 23, 115–123. [Google Scholar] [CrossRef]
- Rowland, M.; Benet, L.Z.; Graham, G.G. Clearance concepts in pharmacokinetics. J. Pharm. Biopharm. 1973, 1, 123–136. [Google Scholar] [CrossRef]
- Davies, B.; Morris, T. Physiological parameters in laboratory animals and humans. Pharm. Res. 1993, 10, 1093–1095. [Google Scholar] [CrossRef] [PubMed]
- Rodighiero, V. Effects of liver disease on pharmacokinetics. An update. Clin. Pharm. 1999, 37, 399–431. [Google Scholar] [CrossRef]
- Breimer, D.D. Pharmacokinetics in liver disease. Pharm. Weekbl. Sci. 1987, 9, 79–84. [Google Scholar] [CrossRef]
- Kim, T.H.; Shin, S.; Shin, B.S. Model-based drug development: Application of modeling and simulation in drug development. J. Pharm. Investig. 2017, 48, 431–441. [Google Scholar] [CrossRef]
- Rowland, M. Physiologic pharmacokinetic models and interanimal species scaling. Pharmacol. Ther. 1985, 29, 49–68. [Google Scholar] [CrossRef]
- Mehvar, R. Clearance Concepts: Fundamentals and Application to Pharmacokinetic Behavior of Drugs. J. Pharm. Pharm. Sci. 2018, 21, 88s–102s. [Google Scholar] [CrossRef]
- Camenisch, G.; Riede, J.; Kunze, A.; Huwyler, J.; Poller, B.; Umehara, K. The extended clearance model and its use for the interpretation of hepatobiliary elimination data. ADMET DMPK 2015, 3, 1–14. [Google Scholar] [CrossRef]
- Camenisch, G.; Umehara, K.-I. Predicting human hepatic clearance from in vitro drug metabolism and transport data: A scientific and pharmaceutical perspective for assessing drug-drug interactions. Biopharm. Drug Dispos. 2012, 33, 179–194. [Google Scholar] [CrossRef]
- Pang, K.S.; Rowland, M. Hepatic Clearance of Drugs. II. Experimental Evidence for Acceptance of the “Well-Stirred” Model over the “Parallel Tube” Model Using Lidocaine in the Perfused Rat Liver in Situ Preparation. J. Pharm. Biopharm. 1977, 5, 655–680. [Google Scholar] [CrossRef]
- Pang, K.S.; Rowland, M. Hepatic clearance of drugs. III. Additional experimental evidence supporting the “wellstirred” model, using metabolite (MEGX) generated from lidocaine under varying hepatic blood flow rates and linear conditions in the perfused rat liverin situ preparation. J. Pharm. Biopharm. 1977, 5, 681–699. [Google Scholar] [CrossRef]
- Pang, K.S.; Rowland, M. Hepatic clearance of drugs. I. Theoretical considerations of a “well-stirred” model and a “parallel tube” model. Influence of hepatic blood flow, plasma and blood cell binding, and the hepatocellular enzymatic activity on hepatic drug clearance. J. Pharm. Biopharm. 1977, 5, 625–653. [Google Scholar] [CrossRef]
- Forker, E.L.; Luxon, B.A. Lumpers vs. distributers. Hepatology 1985, 5, 1236–1237. [Google Scholar] [CrossRef] [PubMed]
- Forker, E.L.; Luxon, B.A. Albumin binding and hepatic uptake: The importance of model selection. J. Pharm. Sci. 1983, 72, 1232–1233. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.S.; Rowland, M. A dispersion model of hepatic elimination: 2. Steady-state considerations-influence of hepatic blood flow, binding within blood, and hepatocellular enzyme activity. J. Pharm. Biopharm. 1986, 14, 261–288. [Google Scholar] [CrossRef]
- Roberts, M.S.; Rowland, M. A dispersion model of hepatic elimination: 1. Formulation of the model and bolus considerations. J. Pharm. Biopharm. 1986, 14, 227–260. [Google Scholar] [CrossRef]
- Sawada, Y.; Sugiyama, Y.; Miyamoto, Y.; Iga, T.; Hanano, M. Hepatic drug clearance model: Comparison among the distributed, parallel-tube and well-stirred models. Chem. Pharm. Bull. 1985, 33, 319–326. [Google Scholar] [CrossRef]
- Bass, L.; Robinson, P.; Bracken, A.J. Hepatic elimination of flowing substrates: The distributed model. J. Biol. 1978, 72, 161–184. [Google Scholar] [CrossRef]
- Weiner, J.G.D. Pharmacokinetic and Pharmacodynamic Data Analysis: Concepts and Applications, 5th ed.; Swedish Pharmaceutical Press: Stockholm, Sweden, 2016. [Google Scholar]
- Gray, M.; Tam, Y. The series-compartment model for hepatic elimination. Drug Metab. Dispos. 1987, 15, 27–31. [Google Scholar]
- Goresky, C.A. Initial distribution and rate of uptake of sulfobromophthalein in the liver. Am. J. Physiol. 1964, 207, 13–26. [Google Scholar] [CrossRef]
- Goresky, C.A.; Bach, G.G.; Nadeau, B.E. Red cell carriage of label: Its limiting effect on the exchange of materials in the liver. Circ. Res. 1975, 36, 328–351. [Google Scholar] [CrossRef] [PubMed]
- Geng, W.P.; Schwab, A.J.; Goresky, C.A.; Pang, K.S. Carrier-mediated uptake and excretion of bromosulfophthalein-glutathione in perfused rat liver: A multiple indicator dilution study. Hepatology 1995, 22, 1188–1207. [Google Scholar] [CrossRef] [PubMed]
- Weiss, M.; Roberts, M.S. Tissue distribution kinetics as determinant of transit time dispersion of drugs in organs: Application of a stochastic model to the rat hindlimb. J. Pharm. Biopharm. 1996, 24, 173–196. [Google Scholar] [CrossRef]
- Lave, T.; Coassolo, P.; Reigner, B. Prediction of hepatic metabolic clearance based on interspecies allometric scaling techniques and in vitro-in vivo correlations. Clin. Pharm. 1999, 36, 211–231. [Google Scholar]
- Rane, A.; Wilkinson, G.; Shand, D. Prediction of hepatic extraction ratio from in vitro measurement of intrinsic clearance. J. Pharm. Exp. 1977, 200, 420–424. [Google Scholar]
- Houston, J.B. Utility of in vitro drug metabolism data in predicting in vivo metabolic clearance. Biochem. Pharm. 1994, 47, 1469–1479. [Google Scholar] [CrossRef]
- Lavé, T.H.; Dupin, S.; Schmitt, C.; Valles, B.; Ubeaud, G.; Chou, R.C.; Jaeck, D.; Coassolo, P. The Use of Human Hepatocytes to Select Compounds Based on Their Expected Hepatic Extraction Ratios in Humans. Pharm. Res. 1997, 14, 152–155. [Google Scholar] [CrossRef]
- Obach, R.S. Prediction of human clearance of twenty-nine drugs from hepatic microsomal intrinsic clearance data: An examination of in vitro half-life approach and nonspecific binding to microsomes. Drug Metab. Dispos. 1999, 27, 1350–1359. [Google Scholar]
- Austin, R.P. The Influence of Nonspecific Microsomal Binding on Apparent Intrinsic Clearance, and Its Prediction from Physicochemical Properties. Drug Metab. Dispos. 2002, 30, 1497–1503. [Google Scholar] [CrossRef] [PubMed]
- Taylor, P. Comprehensive Medicinal Chemistry; Hansch, C., Sammes, P.G., Taylor, J.B., Eds.; Pergamon: New York, NY, USA, 1990; Volume 4. [Google Scholar]
- Howgate, E.M.; Rowland Yeo, K.; Proctor, N.J.; Tucker, G.T.; Rostami-Hodjegan, A. Prediction of in vivo drug clearance from in vitro data. I: Impact of inter-individual variability. Xenobiotica 2006, 36, 473–497. [Google Scholar] [CrossRef]
- Naritomi, Y.; Terashita, S.; Kimura, S.; Suzuki, A.; Kagayama, A.; Sugiyama, Y. Prediction of Human Hepatic Clearance from in Vivo Animal Experiments and in Vitro Metabolic Studies with Liver Microsomes from Animals and Humans. Drug Metab. Dispos. 2001, 29, 1316–1324. [Google Scholar]
- Carlile, D.J.; Zomorodi, K.; Houston, J.B. Scaling factors to relate drug metabolic clearance in hepatic microsome, isolated hepatocytes, and the intact liver. Drug Metab. Dispos. 1997, 25, 903–911. [Google Scholar] [PubMed]
- Iwatsubo, T.; Hirota, N.; Ooie, T.; Suzuki, H.; Shimada, N.; Chiba, K.; Ishizaki, T.; Green, C.E.; Tyson, C.A.; Sugiyama, Y. Prediction of in Viva Drug Metabolism in the Human Liver from in Vitro Metabolism Data. Pharmacol. Ther. 1997, 73, 147–171. [Google Scholar] [CrossRef]
- Nakajima, M.; Nakamura, S.; Tokudome, S.; Shimada, N.; Yamazaki, H.; Yokoi, T. Azelastine N-demethylation by cytochrome P-450 (CYP)3A4, CYP2D6, and CYP1A2 in human liver microsomes: Evaluation of approach to predict the contribution of multiple CYPs. Drug Metab. Dispos. 1999, 27, 1381–1391. [Google Scholar]
- Proctor, N.J.; Tucker, G.T.; Rostami-Hodjegan, A. Predicting drug clearance from recombinantly expressed CYPs: Intersystem extrapolation factors. Xenobiotica 2004, 34, 151–178. [Google Scholar] [CrossRef]
- Berezhkovskiy, L.M. The Corrected Traditional Equations for Calculation of Hepatic Clearance that Account for the Difference in Drug Ionization in Extracellular and Intracellular Tissue Water and the Corresponding Corrected PBPK Equation. J. Pharm. Sci. 2010, 100, 1167–1183. [Google Scholar] [CrossRef]
- Poulin, P.; Kenny, J.R.; Hop, C.E.; Haddad, S. In vitro-in vivo extrapolation of clearance: Modeling hepatic metabolic clearance of highly bound drugs and comparative assessment with existing calculation methods. J. Pharm. Sci. 2012, 101, 838–851. [Google Scholar] [CrossRef] [PubMed]
- Umehara, K.-I.; Camenisch, G. Novel in Vitro-In Vivo Extrapolation (IVIVE) Method to Predict Hepatic Organ Clearance in Rat. Pharm. Res. 2011, 29, 603–617. [Google Scholar] [CrossRef] [PubMed]
- Roots, I.; Gerloff, T.; Meisel, C.; Kirchheiner, J.; Goldammer, M.; Kaiser, R.; Laschinski, G.; Brockmöller, J.; Cascorbi, I.; Kleeberg, U.; et al. Pharmacogenetics-Based New Therapeutic Concepts. Drug Metab. Rev. 2004, 36, 617–638. [Google Scholar] [CrossRef] [PubMed]
- Achour, B.; Barber, J.; Rostami-Hodjegan, A. Expression of hepatic drug-metabolizing cytochrome p450 enzymes and their intercorrelations: A meta-analysis. Drug Metab. Dispos. 2014, 42, 1349–1356. [Google Scholar] [CrossRef] [PubMed]
- Snawder, J.E.; Lipscomb, J.C. Interindividual variance of cytochrome P450 forms in human hepatic microsomes: Correlation of individual forms with xenobiotic metabolism and implications in risk assessment. Regul. Toxicol. Pharm. 2000, 32, 200–209. [Google Scholar] [CrossRef] [PubMed]
- Rostami-Hodjegan, A.; Tucker, G.T. Simulation and prediction of in vivo drug metabolism in human populations from in vitro data. Nat. Rev. Drug Discov. 2007, 6, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Barter, Z.E.; Bayliss, M.K.; Beaune, P.H.; Boobis, A.R.; Carlile, D.J.; Edwards, R.J.; Brian Houston, J.; Lake, B.G.; Lipscomb, J.C.; Pelkonen, O.R.; et al. Scaling Factors for the Extrapolation of in Vivo Metabolic Drug Clearance from In Vitro Data: Reaching a Consensus on Values of Human Micro-somal Protein and Hepatocellularity Per Gram of Liver. Curr. Drug Metab. 2007, 8, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Barter, Z.E.; Chowdry, J.E.; Harlow, J.R.; Snawder, J.E.; Lipscomb, J.C.; Rostami-Hodjegan, A. Covariation of human microsomal protein per gram of liver with age: Absence of influence of operator and sample storage may justify interlaboratory data pooling. Drug Metab. Dispos. 2008, 36, 2405–2409. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, L.; Nguyen, K.; Fretland, A.J. Utility of intersystem extrapolation factors in early reaction phenotyping and the quantitative extrapolation of human liver microsomal intrinsic clearance using recombinant cytochromes P450. Drug Metab. Dispos. 2011, 39, 373–382. [Google Scholar] [CrossRef] [PubMed]
- Venkatakrishnan, K.; von Moltke, L.L.; Court, M.H.; Harmatz, J.S.; Crespi, C.L.; Greenblatt, D.J. Comparison between Cytochrome P450 (CYP) Content and Relative Activity Approaches to Scaling from cDNA-Expressed CYPs to Human Liver Microsomes: Ratios of Accessory Proteins as Sources of Discrepancies between the Approaches. Drug Metab. Dispos. 2000, 28, 1493–1504. [Google Scholar]
- Burczynski, F.J.; Wang, G.Q.; Elmadhoun, B.; She, Y.M.; Roberts, M.S.; Standing, K.G. Hepatocyte [3H]-palmitate uptake: Effect of albumin surface charge modification. Can. J. Physiol. Pharm. 2001, 79, 868–875. [Google Scholar] [CrossRef]
- Poulin, P.; Haddad, S. Toward a new paradigm for the efficient in vitro-in vivo extrapolation of metabolic clearance in humans from hepatocyte data. J. Pharm. Sci. 2013, 102, 3239–3251. [Google Scholar] [CrossRef] [PubMed]
- Poulin, P.; Hop, C.E.; Ho, Q.; Halladay, J.S.; Haddad, S.; Kenny, J.R. Comparative assessment of In Vitro-In Vivo extrapolation methods used for predicting hepatic metabolic clearance of drugs. J. Pharm. Sci. 2012, 101, 4308–4326. [Google Scholar] [CrossRef]
- Hallifax, D.; Houston, J.B. Evaluation of hepatic clearance prediction using in vitro data: Emphasis on fraction unbound in plasma and drug ionisation using a database of 107 drugs. J. Pharm. Sci. 2012, 101, 2645–2652. [Google Scholar] [CrossRef]
- Shitara, Y.; Sato, H.; Sugiyama, Y. Evaluation of drug-drug interaction in the hepatobiliary and renal transport of drugs. Annu. Rev. Pharm. Toxicol. 2005, 45, 689–723. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.-Y.; Benet, L.Z. Predicting Drug Disposition via Application of BCS: Transport/Absorption/Elimination Interplay and Development of a Biopharmaceutics Drug Disposition Classification System. Pharm. Res. 2005, 22, 11–23. [Google Scholar] [CrossRef] [PubMed]
- Kenyon, E.M. Computational Toxicology: Methods in Molecular Biology; Humana Press: Totowa, NJ, USA, 2012; Volume 1, pp. 501–520. [Google Scholar]
- Mahmood, I.; Balian, J.D. Interspecies scaling: Predicting pharmacokinetic parameters of antiepileptic drugs in humans from animals with special emphasis on clearance. J. Pharm. Sci. 1996, 85, 411–414. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.; Hussain, A.; Leal, M.; Mayersohn, M.; Fluhler, E. Interspecies prediction of human drug clearance based on scaling data from one or two animal species. Drug Metab. Dispos. 2007, 35, 1886–1893. [Google Scholar] [CrossRef] [PubMed]
- Boxenbaum, H. Interspecies pharmacokinetic scaling and the evolutionary-comparative paradigm. Drug Metab. Rev. 1984, 15, 1071–1121. [Google Scholar] [CrossRef] [PubMed]
- Goteti, K.; Brassil, P.J.; Good, S.S.; Garner, C.E. Estimation of human drug clearance using multiexponential techniques. J. Clin. Pharm. 2008, 48, 1226–1236. [Google Scholar] [CrossRef]
- Lave, T.; Dupin, S.; Schmitt, C.; Chou, R.C.; Jaeck, D.; Coassolo, P. Integration of in vitro data into allometric scaling to predict hepatic metabolic clearance in man: Application to 10 extensively metabolized drugs. J. Pharm. Sci. 1997, 86, 584–590. [Google Scholar] [CrossRef]
- Hosea, N.A.; Collard, W.T.; Cole, S.; Maurer, T.S.; Fang, R.X.; Jones, H.; Kakar, S.M.; Nakai, Y.; Smith, B.J.; Webster, R.; et al. Prediction of human pharmacokinetics from preclinical information: Comparative accuracy of quantitative prediction approaches. J. Clin. Pharm. 2009, 49, 513–533. [Google Scholar] [CrossRef]
- Ito, K.; Houston, J.B. Prediction of Human Drug Clearance from in Vitro and Preclinical Data Using Physiologically Based and Empirical Approaches. Pharm. Res. 2005, 22, 103–112. [Google Scholar] [CrossRef]
- Nagilla, R.; Ward, K.W. A comprehensive analysis of the role of correction factors in the allometric predictivity of clearance from rat, dog, and monkey to humans. J. Pharm. Sci. 2004, 93, 2522–2534. [Google Scholar] [CrossRef]
- Tang, H.; Mayersohn, M. A novel model for prediction of human drug clearance by allometric scaling. Drug Metab. Dispos. 2005, 33, 1297–1303. [Google Scholar] [CrossRef] [PubMed]
- Wajima, T.; Fukumura, K.; Yano, Y.; Oguma, T. Prediction of human clearance from animal data and molecular structural parameters using multivariate regression analysis. J. Pharm. Sci. 2002, 91, 2489–2499. [Google Scholar] [CrossRef] [PubMed]
- Wajima, T.; Fukumura, K.; Yano, Y.; Oguma, T. Prediction of human pharmacokinetics from animal data and molecular structural parameters using multivariate regression analysis: Oral clearance. J. Pharm. Sci. 2003, 92, 2427–2440. [Google Scholar] [CrossRef] [PubMed]
- Sacher, G.A. Relation of lifespan to brain weight and body weight in mammals. In CIBA Foundation Colloquia on Ageing, Volume 5: The Lifespan of Animals; Little, Brown and Company: Boston, MA, USA, 1959; pp. 115–133. [Google Scholar]
- Mahmood, I. The correction factors do help in improving the prediction of human clearance from animal data. J. Pharm. Sci. 2005, 94, 940–945. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, I. Prediction of Clearance in Humans from In Vitro Human Liver Microsomes and Allometric Scaling. A Comparative Study of the Two Approaches. Drug Metab. Drug Interact. 2002, 19, 49–64. [Google Scholar] [CrossRef]
- Mahmood, I. Interspecies scaling: Predicting oral clearance in humans. Am. J. Ther. 2002, 9, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, I. Interspecies scaling: Role of protein binding in the prediction of clearance from animals to humans. J. Clin. Pharm. 2000, 40 Pt 2, 1439–1446. [Google Scholar]
- Mahmood, I.; Balian, J.D. Interspecies scaling: Predicting clearance of drugs in humans. Three different approaches. Xenobiotica 1996, 26, 887–895. [Google Scholar] [CrossRef]
- Mahmood, I. Prediction of human drug clearance from animal data: Application of the rule of exponents and ‘fu Corrected Intercept Method’ (FCIM). J. Pharm. Sci. 2006, 95, 1810–1821. [Google Scholar] [CrossRef]
- Shiran, M.R.; Proctor, N.J.; Howgate, E.M.; Rowland-Yeo, K.; Tucker, G.T.; Rostami-Hodjegan, A. Prediction of metabolic drug clearance in humans: In vitro-in vivo extrapolation vs allometric scaling. Xenobiotica 2006, 36, 567–580. [Google Scholar] [CrossRef]
- Mahmood, I.; Balian, J.D. Interspecies scaling: A comparative study for the prediction of clearance and volume using two or more than two species. Life Sci. 1996, 59, 579–585. [Google Scholar] [CrossRef]
- Guidance for Industry: M3(R2) Nonclinical Safety Studies for the Conduct of Human Clinical Trials and Marketing Authorization for Pharmaceuticals; U.S. Department of Health and Human Services, Food and Drug Administration (FDA), Center for Drug Evaluation and Research (CDER): Rockville, MD, USA, 2010.
- Mahmood, I.; Sahajwalla, C. Interspecies scaling of biliary excreted drugs. J. Pharm. Sci. 2002, 91, 1908–1914. [Google Scholar] [CrossRef]
- Callan, W.; Sunderman, F., Jr. Species variations in binding of 63 NI (II) by serum albumin. Res. Commun. Mol. Pathol. Pharm. 1973, 5, 459. [Google Scholar]
- Chiou, W.L.; Hsu, F.H. Correlation of Unbound Plasma Clearances of Fifteen Extensively Metabolized Drugs Between Humans and Rats. Pharm. Res. 1988, 05, 668–672. [Google Scholar] [CrossRef]
- Ring, B.J.; Chien, J.Y.; Adkison, K.K.; Jones, H.M.; Rowland, M.; Jones, R.D.; Yates, J.W.; Ku, M.S.; Gibson, C.R.; He, H.; et al. PhRMA CPCDC initiative on predictive models of human pharmacokinetics, part 3: Comparative assessement of prediction methods of human clearance. J. Pharm. Sci. 2011, 100, 4090–4110. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, I. Interspecies Scaling: Predicting Volumes, Mean Residence Time and Elimination Half-life.* Some Suggestions. J. Pharm. Pharm. 1998, 50, 493–499. [Google Scholar] [CrossRef]
- Mahmood, I. Application of allometric principles for the prediction of pharmacokinetics in human and veterinary drug development. Adv. Drug Deliv. Rev. 2007, 59, 1177–1192. [Google Scholar] [CrossRef] [PubMed]
- Berry, L.M.; Li, C.; Zhao, Z. Species differences in distribution and prediction of human V(ss) from preclinical data. Drug Metab. Dispos. 2011, 39, 2103–2116. [Google Scholar] [CrossRef]
- Sawada, Y.; Hanano, M.; Sugiyama, Y.; Iga, T. Prediction of the disposition of nine weakly acidic and six weakly basic drugs in humans from pharmacokinetic parameters in rats. J. Pharm. Biopharm. 1985, 13, 477–492. [Google Scholar] [CrossRef]
- Sawada, Y.; Hanano, M.; Sugiyama, Y.; Iga, T. Prediction of the disposition ofβ-lactam antibiotics in humans from pharmacokinetic parameters in animals. J. Pharm. Biopharm. 1984, 12, 241–261. [Google Scholar] [CrossRef]
- Oie, S.; Tozer, T.N. Effect of altered plasma protein binding on apparent volume of distribution. J. Pharm. Sci. 1979, 68, 1203–1205. [Google Scholar] [CrossRef] [PubMed]
- Obach, R.S.; Baxter, J.G.; Liston, T.E.; Silber, B.M.; Jones, B.C.; Macintyre, F.; Rance, D.J.; Wastall, P. The Prediction of Human Pharmacokinetic Parameters from Preclinical and In Vitro Metabolism Data. J. Pharm. Exp. 1997, 283, 46–58. [Google Scholar]
- Bachmann, K.; Pardoe, D.; White, D. Scaling basic toxicokinetic parameters from rat to man. Environ. Health Perspect. 1996, 104, 400–407. [Google Scholar] [CrossRef]
- Wajima, T.; Fukumura, K.; Yano, Y.; Oguma, T. Prediction of human pharmacokinetics from animal data and molecular structural parameters using multivariate regression analysis: Volume of distribution at steady state. J. Pharm. Pharm. 2003, 55, 939–949. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Ma, X.; Liu, Y.; Zhou, H.; Shi, C.; Wu, F.; Jiang, J.; Hu, P. Quantitative prediction of human pharmacokinetics and pharmacodynamics of imigliptin, a novel DPP-4 inhibitor, using allometric scaling, IVIVE and PK/PD modeling methods. Eur. J. Pharm. Sci. 2016, 89, 73–82. [Google Scholar] [CrossRef]
- Winiwarter, S.; Bonham, N.M.; Ax, F.; Hallberg, A.; Lennernas, H.; Karlen, A. Correlation of human jejunal permeability (in vivo) of drugs with experimentally and theoretically derived parameters. A multivariate data analysis approach. J. Med. Chem. 1998, 41, 4939–4949. [Google Scholar] [CrossRef]
- Sun, D.; Lennernas, H.; Welage, L.S.; Barnett, J.L.; Landowski, C.P.; Foster, D.; Fleisher, D.; Lee, K.D.; Amidon, G.L. Comparison of human duodenum and Caco-2 gene expression profiles for 12,000 gene sequences tags and correlation with permeability of 26 drugs. Pharm. Res. 2002, 19, 1400–1416. [Google Scholar] [CrossRef] [PubMed]
- Sinko, P.J.; Leesman, G.D.; Amidon, G.L. Predicting Fraction Dose Absorbed in Humans Using a Macroscopic Mass Balance Approach. Pharm. Res. 1991, 8, 979–988. [Google Scholar] [CrossRef]
- Usansky, H.H.; Sinko, P.J. Estimating human drug oral absorption kinetics from Caco-2 permeability using an absorption-disposition model: Model development and evaluation and derivation of analytical solutions for k(a) and F(a). J. Pharm. Exp. 2005, 314, 391–399. [Google Scholar] [CrossRef]
- Yu, L.X.; Amidon, G.L. A compartmental absorption and transit model for estimating oral drug absorption. Int. J. Pharm. 1999, 186, 119–125. [Google Scholar] [CrossRef]
- Lennernäs, H.; Ahrenstedt, Ö.; Hällgren, R.; Knutson, L.; Ryde, M.; Paalzow, L.K. Regional Jejunal Perfusion, a New in Vivo Approach to Study Oral Drug Absorption in Man. Pharm. Res. 1992, 9, 1243–1251. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.X.; Crison, J.R.; Amidon, G.L. Compartmental transit and dispersion model analysis of small intestinal transit flow in humans. Int. J. Pharm. 1996, 140, 111–118. [Google Scholar] [CrossRef]
- Mukkavilli, R.; Pinjari, J.; Patel, B.; Sengottuvelan, S.; Mondal, S.; Gadekar, A.; Verma, M.; Patel, J.; Pothuri, L.; Chandrashekar, G.; et al. In vitro metabolism, disposition, preclinical pharmacokinetics and prediction of human pharmacokinetics of DNDI-VL-2098, a potential oral treatment for Visceral Leishmaniasis. Eur. J. Pharm. Sci. 2014, 65, 147–155. [Google Scholar] [CrossRef] [PubMed]


| Model | Scheme 1 | CLH 2 | ERH |
|---|---|---|---|
| Well-stirred |  | ||
| Parallel tube |  | ||
| Distributed |  | ||
| Dispersion |  |
| Equation | Comment * | Ref. | |
|---|---|---|---|
| (38) | Basic principle of IVIVE was suggested Provide the 4 stages for the IVIVE | [60] | |
| (39) | |||
| (40) | Empirically the scaling factor (SF) was estimated as the value of 8.9 Predicted ERH and observed ERH are ERH, pred and ERH, obs, respectively Provide criteria for the classification of the drugs into: low extraction, ERH < 0.3; intermediate, 0.3 < ERH < 0.7; high extraction, ERH > 0.7 | [61] | |
| (41) | |||
| (42) | |||
| (43) | Investigation of the effect of the protein binding into the plasma and microsomes The ISTD refers to the internal standard | [62] | |
| (44) | |||
| (45) | Animal scaling factor was incorporated into IVIVE | [66] | |
| (46) | |||
| (47) | |||
| (48) | Microsomal protein recovery (MPR) ratio was incorporated in IVIVE RB/P refers to blood to plasma ratio | [67] | |
| (49) | |||
| (50) | |||
| (51) | CYP abundance was incorporated in IVIVE | [68] | |
| (52) | Relative activity factor (RAF) introduced for scaling rhCYP data to HLM Modified RAF taking into account of Km | [69,70] | |
| (53) | |||
| (54) | |||
| (55) | Inter-system extrapolation factor (ISEF) is introduced for scaling rhCYP data to HLM | [69] | |
| (56) | |||
| (57) | The ionization factor is incorporated into the IVIVE FI is an ionization factor Subscript letter IW denotes intracellular water Upper letter i and n indicate compounds of ionized and neutral forms, respectively | [71] | |
| (58) | |||
| (59) | |||
| (60) | |||
| (61) | The unbound fraction into the liver (fu,liver) is incorporated into the IVIVE Plasma to whole liver concentration ratio (PLR) = 13.3 | [72] | |
| (62) | |||
| (63) | Physiologically-based IVIVE model Total apparent uptake clearance (PSuptake,total) consists of saturable and/or non-saturable processes CLmet and PSbile refer to metabolic and biliary clearance, respectively Apparent sinusoidal total efflux clearance from the intracellular side of hepatocytes back into blood (PSefflux, total) consists of saturable and/or non-saturable processes | [73] | |
| (64) | |||
| (65) | Provide the method for the prediction of total clearance and relative elimination contributions The fnH, fnsec, and fnmet refers to a fractional contribution of hepatic, biliary, and metabolic elimination to overall clearance PSinf, act and PSinf, pas refer to the sinusoidal active and passive influx clearance, respectively Sinusoidal efflux from hepatocytes back into blood (PSeff) is assumed to occur via passive diffusion, therefore PSeff = PSinf,pas CLint,sec and CLint,met refer to intrinsic secretory and metabolic clearance, respectively PSinf equals to the sum of PSinf,act and PSinf,pas which are determined by suspension of pooled human hepatocytes (unit: mL/min/kg) | [8] | |
| (66) | |||
| (67) | |||
| (68) | |||
| (69) | |||
| (70) | |||
| (71) |
| Method | Equation | Comments * | Ref. | |
|---|---|---|---|---|
| Simple AS | (74) | Select a proper equation by the rule of exponent (ROE) W and BW represent body and brain weight, respectively | - | |
| AS with MLP 1 | (75) | - | ||
| AS with BW | (76) | [89] | ||
| Rule of exponent | If the exponent is 0.55 to 0.7, then use the simple AS, Equation (74) | [90] | ||
| If the exponent is 0.71 to 1, then use the MLP, Equation (75) | ||||
| If the exponent is more than 1, then use the BW, Equation (76) | ||||
| Two-term method | (77) | θ is a constant, which is determined by multiple regression analysis | [91] | |
| Multiexponential | (78) | The unit of CL is mL/min | [92] | |
| Normalized AS | (79) | CLint refers the unbound CLint in microsomes or hepatocytes in species and humans | [93] | |
| One species AS | (80) | The exponent b is a constant 0.75, which is physiologically relevant value (e.g., blood flow, filtration, etc.) | [94,95] | |
| One species AS | (81) | Predict the CL of bound drug | [90] | |
| (82) | ||||
| (83) | ||||
| Two species AS | (84) | Predict the CL of bound drug | ||
| (85) | ||||
| Hepatic liver method | (86) | [96] | ||
| FCIM 2 | (87) | Rfu is the fu ratio between rats and humans and a is the coefficient form AS The unit of CL is mL/min | [97] | |
| QSAR 3 | (88) | The unit of observed and predicted CL value is mL/min/kg | [98] | |
| (89) | The unit of observed and predicted oral CL value is mL/min/kg | [99] | ||
| Method | Equation | Comment * | Ref. | |
|---|---|---|---|---|
| Simple AS | (93) | The prediction of Vd is well predicted equally with using two species in AS | [108] | |
| Average fraction unbound in tissue 1 | (94) | It is useful to analyze and predict an alteration in apparent Vd then identify the cause of alteration. It is particularly useful for drugs with low Vd (<15 L or 0.2 L/kg) | [119] | |
| Proportionality | (95) | It is assumed that the volume of distribution at a steady state of free drug is identical between species | [120] | |
| One species AS | (96) | Statistical modeling is applied in this model | [121] | |
| QSAR | (97) | Vdss, human (mL/kg) is predicted by QSAR modeling with quadratic term descriptors | [122] | |
| Method | Equation | Comments * | Ref. | |
|---|---|---|---|---|
| AS | (102) | The unit of ka is h in time−1 | [88] | |
| QSAR1 | (103) | The choice of model for prediction depends on the availability of descriptor data Effective permeability in 10−4 cm/s | [124] | |
| (104) | ||||
| (105) | ||||
| Use of Caco2 data 2 | (106) | All tested drugs | [125] | |
| (107) | ||||
| (108) | Only passively diffused drugs | |||
| (109) | ||||
| (110) | Only carrier-mediated drugs | |||
| (111) | ||||
| Sinko et al. 5 | (112) | The absorption rate constant is proportional to the Peff | [126] | |
| Mechanism based modeling 3 | (113) | Fa is expressed as percent unit The equation is the result of the correlation between Fa,pred and Fa,exp | [127] | |
| (114) | ka,eq is expressed as the unit of min−1 ka,eq is a key determinant for Fa and can be used as PK modeling | |||
| (115) | ||||
| Compartmental absorption and transit model 4 | (116) | Fa is expressed as the fractional value. | [128] | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, G.-W.; Lee, Y.-B.; Cho, H.-Y. Interpretation of Non-Clinical Data for Prediction of Human Pharmacokinetic Parameters: In Vitro-In Vivo Extrapolation and Allometric Scaling. Pharmaceutics 2019, 11, 168. https://doi.org/10.3390/pharmaceutics11040168
Choi G-W, Lee Y-B, Cho H-Y. Interpretation of Non-Clinical Data for Prediction of Human Pharmacokinetic Parameters: In Vitro-In Vivo Extrapolation and Allometric Scaling. Pharmaceutics. 2019; 11(4):168. https://doi.org/10.3390/pharmaceutics11040168
Chicago/Turabian StyleChoi, Go-Wun, Yong-Bok Lee, and Hea-Young Cho. 2019. "Interpretation of Non-Clinical Data for Prediction of Human Pharmacokinetic Parameters: In Vitro-In Vivo Extrapolation and Allometric Scaling" Pharmaceutics 11, no. 4: 168. https://doi.org/10.3390/pharmaceutics11040168