A Cell-Level Systems PK-PD Model to Characterize In Vivo Efficacy of ADCs
Abstract
:1. Introduction
2. Materials and Methods
2.1. Cell Lines
2.2. Tool ADC
2.3. Development of Xenograft Mouse Models
2.4. Development of Bioanalytical Techniques
2.5. Tumor Pharmacokinetic Studies
2.6. Tumor Growth Inhibition Studies
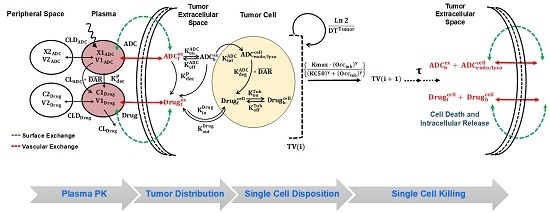
2.7. Development of In-Vivo systems PK-PD Model for T-vc-MMAE ADC
2.7.1. Plasma PK Model for ADC
2.7.2. Tumor Distribution Model for ADC
2.7.3. Single Cell Disposition Model for ADC
2.7.4. Characterization of Intracellular Occupancy of Tubulin with MMAE
2.7.5. Linking Intracellular Occupancy of Tubulin to Tumor-Growth Inhibition
3. Parameter Estimation, Model Fitting and Simulations
4. Results
4.1. Plasma and Tumor PK Studies:
4.2. Tumor Growth Inhibition Studies:
4.3. Development of the Systems PK-PD Model for ADC:
4.3.1. Plasma PK Model for T-vc-MMAE:
4.3.2. Tumor Distribution Model for T-vc-MMAE
4.3.3. Prediction of Intracellular Occupancy of Tubulin
4.3.4. Linking Intracellular Tubulin Occupancy to Tumor Growth Inhibition
5. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lambert, J.M. Antibody-Drug Conjugates (ADCs): Magic Bullets at Last! Mol. Pharm. 2015, 12, 1701–1702. [Google Scholar] [CrossRef] [PubMed]
- Van Geel, R.; Wijdeven, M.A.; Heesbeen, R.; Verkade, J.M.; Wasiel, A.A.; van Berkel, S.S.; van Delft, F.L. Chemoenzymatic Conjugation of Toxic Payloads to the Globally Conserved N-Glycan of Native mAbs Provides Homogeneous and Highly Efficacious Antibody-Drug Conjugates. Bioconjug. Chem. 2015, 26, 2233–2242. [Google Scholar] [CrossRef] [PubMed]
- Tumey, L.N.; Li, F.; Rago, B.; Han, X.; Loganzo, F.; Musto, S.; Clark, T. Site Selection: A Case Study in the Identification of Optimal Cysteine Engineered Antibody Drug Conjugates. AAPS J. 2017, 19, 1123–1135. [Google Scholar] [CrossRef] [PubMed]
- Mantaj, J.; Jackson, P.J.; Rahman, K.M.; Thurston, D.E. From Anthramycin to Pyrrolobenzodiazepine (PBD)-Containing Antibody-Drug Conjugates (ADCs). Angew Chem. Int. Ed. Engl. 2017, 56, 462–488. [Google Scholar] [CrossRef] [PubMed]
- Anthony, L.; Kumar, R. Review of the ADC Clinical Pipeline. In Proceedings of the World ADC Summit, Berlin, Germany, 26–28 March 2018. [Google Scholar]
- Zhao, H.; Atkinson, J.; Gulesserian, S.; Zeng, Z.; Nater, J.; Ou, J.; Challita-Eid, P. Modulation of Macropinocytosis-Mediated Internalization Decreases Ocular Toxicity of Antibody-Drug Conjugates. Cancer Res. 2018, 78, 2115–2126. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Shin, Y.G.; Shah, D.K. Application of Pharmacokinetic-Pharmacodynamic Modeling and Simulation for Antibody-Drug Conjugate Development. Pharm. Res. 2015, 32, 3508–3525. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Shah, D.K. Utility of PK-PD Modeling and Simulation to Improve Decision Making for Antibody-Drug Conjugate Development. In Innovations for Next-Generation Antibody-Drug Conjugates Cancer Drug Discovery and Development; Damelin, M., Ed.; Humana Press: New York, NY, USA, 2018. [Google Scholar]
- Khot, A.; Sharma, S.; Shah, D.K. Integration of bioanalytical measurements using PK-PD modeling and simulation: Implications for antibody-drug conjugate development. Bioanalysis 2015, 7, 1633–1648. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Shah, D.K. Application of a PK-PD Modeling and Simulation-Based Strategy for Clinical Translation of Antibody-Drug Conjugates: A Case Study with Trastuzumab Emtansine (T-DM1). AAPS J. 2017, 19, 1054–1070. [Google Scholar] [CrossRef] [PubMed]
- Shah, D.K.; Haddish-Berhane, N.; Betts, A. Bench to bedside translation of antibody drug conjugates using a multiscale mechanistic PK/PD model: A case study with brentuximab-vedotin. J Pharmacokinet Pharmacodyn. 2012, 39, 643–659. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Maass, K.F.; Betts, A.M.; Wittrup, K.D.; Kulkarni, C.; King, L.E.; Khot, A.; Shah, D.K. Evolution of Antibody-Drug Conjugate Tumor Disposition Model to Predict Preclinical Tumor Pharmacokinetics of Trastuzumab-Emtansine (T-DM1). AAPS J. 2016, 18, 861–875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shah, D.K.; King, L.E.; Han, X.; Wentland, J.A.; Zhang, Y.; Lucas, J.; Haddish-Berhane, N.; Betts, A.; Leal, M. A priori prediction of tumor payload concentrations: Preclinical case study with an auristatin-based anti-5T4 antibody-drug conjugate. AAPS J. 2014, 16, 452–463. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Shah, D.K. Measurement and Mathematical Characterization of Cell-Level Pharmacokinetics of Antibody-Drug Conjugates: A Case Study with Trastuzumab-vc-MMAE. Drug Metab. Dispos. 2017, 45, 1120–1132. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Shah, D.K. A ‘Dual’ Cell-Level Systems PK-PD Model to Characterize the Bystander Effect of ADC. J. Pharm. Sci. 2019, in press. [Google Scholar]
- Singh, A.P.; Sharma, S.; Shah, D.K. Quantitative characterization of in vitro bystander effect of antibody-drug conjugates. J. Pharmacokinet Pharmacodyn 2016, 43, 567–582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donoghue, J.F.; McGavigan, C.J.; Lederman, F.L.; Cann, L.M.; Fu, L.; Dimitriadis, E.; Girling, G.E.; Rogers, P.A.W. Dilated thin-walled blood and lymphatic vessels in human endometrium: A potential role for VEGF-D in progestin-induced break-through bleeding. PLoS ONE 2012, 7, e30916. [Google Scholar] [CrossRef] [PubMed]
- Thurber, G.M.; Schmidt, M.M.; Wittrup, K.D. Antibody tumor penetration: Transport opposed by systemic and antigen-mediated clearance. Adv. Drug Deliv. Rev. 2008, 60, 1421–1434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thurber, G.M.; Schmidt, M.M.; Wittrup, K.D. Factors determining antibody distribution in tumors. Trends Pharmacol. Sci. 2008, 29, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.M.; Wittrup, K.D. A modeling analysis of the effects of molecular size and binding affinity on tumor targeting. Mol. Cancer Ther. 2009, 8, 2861–2871. [Google Scholar] [CrossRef] [PubMed]
- Monte, U.D. Does the cell number 109 still really fit one gram of tumor tissue? Cell Cycle. 2009, 8, 505–506. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Mager, D.E.; Straubinger, R.M. Comparison of two pharmacodynamic transduction models for the analysis of tumor therapeutic responses in model systems. AAPS J. 2010, 12, 1–10. [Google Scholar] [CrossRef] [PubMed]
- D’Argenio David, Z.; Alan, S.; Xiaoning, W. ADAPT 5 User’s Guide: Pharmacokinetic/Pharmacodynamic Systems Analysis Software; Biomedical Simulations Resource: Los Angeles, CA, USA, 2009. [Google Scholar]
- Lavielle, M.; Mentre, F. Estimation of population pharmacokinetic parameters of saquinavir in HIV patients with the MONOLIX software. J. Pharmacokinet Pharmacodyn 2007, 34, 229–249. [Google Scholar] [CrossRef] [PubMed]
- Bazin, R.; Boucher, G.; Monier, G.; Chevrier, M.C.; Verrette, S.; Broly, H.; Lemieux, R. Use of hu-IgG-SCID mice to evaluate the in vivo stability of human monoclonal IgG antibodies. J. Immunol. Methods 1994, 172, 209–217. [Google Scholar] [CrossRef]
- Figueroa, I.; Leipold, D.; Leong, S.; Zheng, B.; Triguero-Carrasco, M.; Fourie-O’Donohue, A.; Kozak, K.R.; Xu, K.; Schutten, M.; Wang, H.; et al. Prediction of non-linear pharmacokinetics in humans of an antibody-drug conjugate (ADC) when evaluation of higher doses in animals is limited by tolerability: Case study with an anti-CD33 ADC. MAbs 2018, 10, 738–750. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.P.; Krzyzanski, W.; Martin, S.W.; Weber, G.; Betts, A.; Ahmad, A.; Abraham, A.; Zutshi, A.; Lin, J.; Singh, P. Quantitative prediction of human pharmacokinetics for mAbs exhibiting target-mediated disposition. AAPS J. 2015, 17, 389–399. [Google Scholar] [CrossRef] [PubMed]
- Cilliers, C.; Guo, H.; Liao, J.; Christodolu, N.; Thurber, G.M. Multiscale Modeling of Antibody-Drug Conjugates: Connecting Tissue and Cellular Distribution to Whole Animal Pharmacokinetics and Potential Implications for Efficacy. AAPS J. 2016, 18, 1117–1130. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, W.; Wang, E.Q.; Balthasar, J.P. Monoclonal antibody pharmacokinetics and pharmacodynamics. Clin. Pharmacol. Ther. 2008, 84, 548–558. [Google Scholar] [CrossRef] [PubMed]
- Betts, A.M.; Haddish-Berhane, N.; Tolsma, J.; Jasper, P.; King, L.E.; Sun, Y.; Chakrapani, S.; Shor, B.; Boni, J.; Johnson, P.R. Preclinical to Clinical Translation of Antibody-Drug Conjugates Using PK/PD Modeling: A Retrospective Analysis of Inotuzumab Ozogamicin. AAPS J. 2016, 18, 1101–1116. [Google Scholar] [CrossRef] [PubMed]






| Parameter | Definition | Value (CV %) | Unit | Source |
|---|---|---|---|---|
| Parameters associated with plasma pharmacokinetics of T-vc-MMAE | ||||
| , | Central and distributional clearances of T-vc-MMAE | 0.033 (4.8%), 0.0585 (12.6%) | L/day/Kg | Estimated |
| , | Central and peripheral volumes of distribution for T-vc-MMAE | 0.084 (7.3%), 0.051 (5.2%) | L/Kg | Estimated |
| , | Central and distributional clearances of free MMAE | 18.40, 1.84 | L/day/Kg | [11] |
| , | Central and peripheral volumes of distribution for T-vc-MMAE | 0.136, 0.523 | L/Kg | [11] |
| Non-specific deconjugation of MMAE from T-vc-MMAE | 0.323 (8.8%) | 1/day | Estimated | |
| Parameters associated with tumor distribution of T-vc-MMAE | ||||
| Radius of the tumor blood capillary | 8.0 | µm | [18,19,20] | |
| An average distance between two capillaries | 75.0 | µm | [18,19,20] | |
| , | The rates of permeability of T-vc-MMAE and MMAE across the blood vessels respectively | 334, 21000 | µm/day | [18,19,20] |
| , | The rates of diffusion of T-vc-MMAE and MMAE across the blood vessels respectively | 0.022, 0.25 | cm2/day | [18,19,20] |
| , | Tumor void volume for T-vc-MMAE and MMAE | 0.24, 0.44 | Unitless | [18,19,20] |
| Radius of a spherical tumor calculated based on varying tumor volume (TV) where: | Dynamic | cm | ||
| Parameters associated with single cell disposition of T-vc-MMAE | ||||
| Second order association rate constant between T-vc-MMAE and HER2 receptor | 0.03 | 1/nM/h | [14] | |
| First order dissociation rate constant between T-vc-MMAE and HER2 receptor | 0.014 | 1/h | [14] | |
| Internalization rate of HER2-ADC complex inside the cell | 0.11 | 1/h | [14] | |
| Intracellular degradation of T-vc-MMAE in endosomal/lysosomal space | 0.353 | 1/h | [14] | |
| Second order association rate constant between cytoplasmic MMAE and intracellular tubulin protein | 0.0183 | 1/nM/h | [14] | |
| First order dissociation rate constant between MMAE-tubulin complex | 0.545 | 1/h | [14] | |
| Total concentration of intracellular tubulin in a single cell | 65 | nM | [11,14] | |
| First order influx rate of MMAE from extracellular to intracellular space | 8.33 | 1/h | [14] | |
| First order efflux rate of MMAE from intracellular to extracellular space | 0.046 | 1/h | [11] | |
| , | Model estimated HER2 receptor count on each tumor cell in N87 and GFP-MCF7 tumors in vivo | 185,000 (2.8%), 22,400 (3.2%) | Numbers/Cell | Estimated |
| Parameters associated with single cell killing of T-vc-MMAE in tumors | ||||
| First order killing rate of MMAE in each tumor cell (either GFP-MCF7 or N87) | 1.03 (31.3%) | 1/day | Estimated | |
| Percentage of intracellular occupancy to tubulin by MMAE which leads to 50% of maximum killing | 96.8 (13.2%) | Percentage | Estimated | |
| Transit time associated with the killing | 2.03 | Day | Estimated | |
| , | Inter-subject variability associated with Kmax and ‘Tau’ values assuming log-normal distribution | 10.16 (47%), 19.4 (32%) | Percentage | Estimated |
| Curve-fitting parameter associated with sigmoidal tubulin occupancy-killing relationship | 15.02 (38.6%) | Unitless | Estimated | |
| , | Doubling time of N87 and GFP-MCF7 tumors | 13.5 (11.4%), 10.6 (18.7%) | Day | Estimated |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.P.; Guo, L.; Verma, A.; Wong, G.G.-L.; Shah, D.K. A Cell-Level Systems PK-PD Model to Characterize In Vivo Efficacy of ADCs. Pharmaceutics 2019, 11, 98. https://doi.org/10.3390/pharmaceutics11020098
Singh AP, Guo L, Verma A, Wong GG-L, Shah DK. A Cell-Level Systems PK-PD Model to Characterize In Vivo Efficacy of ADCs. Pharmaceutics. 2019; 11(2):98. https://doi.org/10.3390/pharmaceutics11020098
Chicago/Turabian StyleSingh, Aman P., Leiming Guo, Ashwni Verma, Gloria Gao-Li Wong, and Dhaval K. Shah. 2019. "A Cell-Level Systems PK-PD Model to Characterize In Vivo Efficacy of ADCs" Pharmaceutics 11, no. 2: 98. https://doi.org/10.3390/pharmaceutics11020098