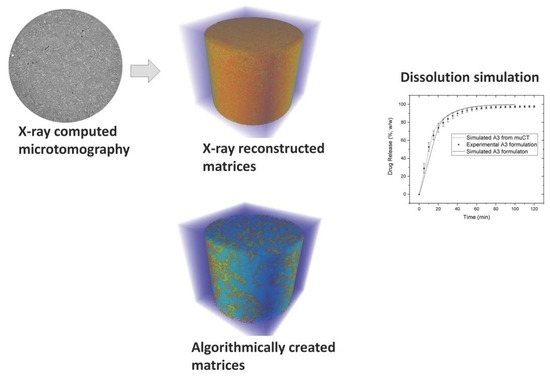
Modeling of Disintegration and Dissolution Behavior of Mefenamic Acid Formulation Using Numeric Solution of Noyes-Whitney Equation with Cellular Automata on Microtomographic and Algorithmically Generated Surfaces
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Preparation of Tablets
2.2.2. Determination of Tablet Porosity and Tensile Strength
2.2.3. Measurement of Granule Size Distribution
2.2.4. X-Ray Microtomography
2.2.5. Disintegration Test
2.2.6. Dissolution Test
2.3. Simulation of Drug Release with Cellular Automata
2.3.1. Application of Noyes-Whitney Equation in Numeric Calculation of Drug Dissolution
- As soon as a disintegrant cell is signaled to get in contact with a medium-type voxel, its state is converted to “active”.
- All “active” disintegrant cells mark their direct neighbors for random scattering within the calculation matrix. The labeling depth, i.e., radius around the active disintegrant particles, can be set through the simulations parameter (C2).
- All marked cells are randomly distributed in the surrounding medium to maximize the contact surface to the liquid.
- As soon as the disintegrant cell is “activated”, it loses its action; therefore, the random scattering of its neighborhood can be fired only once.
- Rule: If a cell has three positive neighbors, then, on the next epoch, this cell becomes positive.
- Rule: If a cell has two positive neighbors, then, on the next epoch, this cell remains unchanged.
2.3.2. Matrix Arrangement of Tablets
2.3.3. Comparison of Drug Release Pattern between Experimental and Simulated Profiles
3. Results
3.1. In Vitro Evaluation of Drug Release
3.2. Granule Size Distribution Experimentally Measured and Designed in Simulation Matrices
3.3. Comparison between In Vitro and In Silico Drug Release Profiles
3.4. In Silico Evaluation of Drug Release
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug dissolution. Int. J. Pharm. 2013, 453, 12–24. [Google Scholar] [CrossRef] [PubMed]
- Macheras, P.; Iliadis, A. Modeling in Biopharmaceutics, Pharmacokinetics, and Pharmacodynamics; Interdisciplinary Applied Mathematics; Springer: New York, NY, USA, 2006; Volume 30, ISBN 0-387-28178-9. [Google Scholar]
- Wu, C.-Y.; Ruddy, O.M.; Bentham, A.C.; Hancock, B.C.; Best, S.M.; Elliott, J.A. Modelling the mechanical behaviour of pharmaceutical powders during compaction. Powder Technol. 2005, 152, 107–117. [Google Scholar] [CrossRef]
- Lamberti, G.; Galdi, I.; Barba, A.A. Controlled release from hydrogel-based solid matrices. A model accounting for water up-take, swelling and erosion. Int. J. Pharm. 2011, 407, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Kimber, J.A.; Kazarian, S.G.; Štěpánek, F. DEM simulation of drug release from structurally heterogeneous swelling tablets. Powder Technol. 2013, 248, 68–76. [Google Scholar] [CrossRef]
- Kimber, J.A.; Kazarian, S.G.; Štěpánek, F. Modelling of pharmaceutical tablet swelling and dissolution using discrete element method. Chem. Eng. Sci. 2012, 69, 394–403. [Google Scholar] [CrossRef]
- Kimber, J.A.; Kazarian, S.G.; Štěpánek, F. Formulation design space analysis for drug release from swelling polymer tablets. Powder Technol. 2013, 236, 179–187. [Google Scholar] [CrossRef]
- Kimber, J.A.; Kazarian, S.G.; Štěpánek, F. Microstructure-based mathematical modelling and spectroscopic imaging of tablet dissolution. Comput. Chem. Eng. 2011, 35, 1328–1339. [Google Scholar] [CrossRef]
- Thornton, C.; Ciomocos, M.T.; Adams, M.J. Numerical simulations of agglomerate impact breakage. Powder Technol. 1999, 105, 74–82. [Google Scholar] [CrossRef]
- Mishra, B.K.; Thornton, C. Impact breakage of particle agglomerates. Int. J. Miner. Process. 2001, 61, 225–239. [Google Scholar] [CrossRef]
- Bagherzadeh-Khalkhali, A.; Mirghasemi, A.A.; Mohammadi, S. Micromechanics of breakage in sharp-edge particles using combined DEM and FEM. Particuology 2008, 6, 347–361. [Google Scholar] [CrossRef]
- Frenning, G. An efficient finite/discrete element procedure for simulating compression of 3D particle assemblies. Comput. Methods Appl. Mech. Eng. 2008, 197, 4266–4272. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; AM Ende, M.T.; Hancock, B.C. Process modeling in the pharmaceutical industry using the discrete element method. J. Pharm. Sci. 2009, 98, 442–470. [Google Scholar] [CrossRef] [PubMed]
- Kodam, M.; Curtis, J.; Hancock, B.; Wassgren, C. Discrete element method modeling of bi-convex pharmaceutical tablets: Contact detection algorithms and validation. Chem. Eng. Sci. 2012, 69, 587–601. [Google Scholar] [CrossRef]
- Rybacki, S.; Himmelspach, J.; Uhrmacher, A.M. Experiments with Single Core, Multi-core, and GPU Based Computation of Cellular Automata. In Proceedings of the 2009 First International Conference on Advances in System Simulation, Porto, Portugal, 20–25 September 2009; pp. 62–67. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; Volume 30, ISBN 1-579-55008-8. [Google Scholar]
- Puchkov, M.; Tschirky, D.; Leuenberger, H. 3-D cellular automata in computer-aided design of pharmaceutical formulations: Mathematical concept and F-CAD software. In Formulation Tools for Pharmaceutical Development; Elsevier B.V.: Amsterdam, The Netherlands, 2013; pp. 155–201. ISBN 9781907568992. [Google Scholar]
- Laaksonen, H.; Hirvonen, J.; Laaksonen, T. Cellular automata model for swelling-controlled drug release. Int. J. Pharm. 2009, 380, 25–32. [Google Scholar] [CrossRef] [PubMed]
- Kimura, G.; Puchkov, M.; Leuenberger, H. An attempt to calculate in silico disintegration time of tablets containing mefenamic acid, a low water-soluble drug. J. Pharm. Sci. 2013, 102, 2166–2178. [Google Scholar] [CrossRef] [PubMed]
- Eberle, V.A.; Schoelkopf, J.; Gane, P.A.C.; Alles, R.; Huwyler, J.; Puchkov, M. Floating gastroretentive drug delivery systems:Comparison of experimental and simulated dissolution profiles and floatation behavior. Eur. J. Pharm. Sci. 2014, 58, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Eberle, V.A.; Häring, A.; Schoelkopf, J.; Gane, P.A.C.; Huwyler, J.; Puchkov, M. In silico and in vitro methods to optimize the performance of experimental gastroretentive floating mini-tablets In silico and in vitro methods to optimize the performance of experimental gastroretentive floating mini-tablets. Drug Dev. Ind. Pharm. 2016, 42, 808–817. [Google Scholar] [CrossRef] [PubMed]
- Park, S.-H.; Choi, H.-K. The effects of surfactants on the dissolution profiles of poorly water-soluble acidic drugs. Int. J. Pharm. 2006, 321, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Razvi, N.; Siddiqui, S.A.; Khan, L.G. The effect of surfactant on the dissolution rate of ibuprofen tablets. Int. Chem. Pharm. Med. J. 2005, 2, 213–216. [Google Scholar]
- Kitamori, N.; Makino, T. Effect of drug content and drug particle size on the change in particle size during tablet compression. J. Pharm. Pharmacol. 1979, 31, 505–507. [Google Scholar] [CrossRef] [PubMed]
- Yekpe, K.; Abatzoglou, N.; Bataille, B.; Gosselin, R.; Sharkawi, T.; Simard, J.-S.; Cournoyer, A. Predicting the dissolution behavior of pharmaceutical tablets with NIR chemical imaging. Int. J. Pharm. 2015, 486, 242–251. [Google Scholar] [CrossRef] [PubMed]
- Ghayas, S.; Sheraz, M.A.; Anjum, F.; Baig, M.T. Factors influencing the dissolution testing of drugs. Pak. J. Heal. Res. 2013, 1, 1–11. [Google Scholar]
- Yen, J.K. The dissolution rate principle in practical tablet formulation. Can. Pharm. J. 1964, 97, 493–499. [Google Scholar]
- Desai, P.M.; Liew, C.V.; Heng, P.W.S. Review of Disintegrants and the Disintegration Phenomena. J. Pharm. Sci. 2016, 105, 2545–2555. [Google Scholar] [CrossRef] [PubMed]
- Steendam, R.; Frijlink, H.W.; Lerk, C.F. Plasticisation of amylodextrin by moisture. Consequences for compaction behaviour and tablet properties. Eur. J. Pharm. Sci. 2001, 14, 245–254. [Google Scholar] [CrossRef]
- Sinka, I.C.; Burch, S.F.; Tweed, J.H.; Cunningham, J.C. Measurement of density variations in tablets using X-ray computed tomography. Int. J. Pharm. 2004, 271, 215–224. [Google Scholar] [CrossRef] [PubMed]
- Busignies, V.; Leclerc, B.; Porion, P.; Evesque, P.; Couarraze, G.; Tchoreloff, P. Quantitative measurements of localized density variations in cylindrical tablets using X-ray microtomography. Eur. J. Pharm. Biopharm. 2006, 64, 38–50. [Google Scholar] [CrossRef] [PubMed]
- Pajander, J.; van Veen, B.; Korhonen, O.; Lappalainen, R.; Ketolainen, J. Liquid boundary movements in cylindrical and convex hydrophobic matrix tablets: Effects on tablet cracking and drug release. Eur. J. Pharm. Biopharm. 2006, 64, 167–172. [Google Scholar] [CrossRef] [PubMed]
- Westermarck, S.; Juppo, A.M.; Kervinen, L.; Yliruusi, J. Pore structure and surface area of mannitol powder, granules and tablets determined with mercury porosimetry and nitrogen adsorption. Eur. J. Pharm. Biopharm. 1998, 46, 61–68. [Google Scholar] [CrossRef]
- Smrčka, D.; Dohnal, J.; Štěpánek, F. Dissolution and disintegration kinetics of high-active pharmaceutical granules produced at laboratory and manufacturing scale. Eur. J. Pharm. Biopharm. 2016, 106, 107–116. [Google Scholar] [CrossRef] [PubMed]
- Shah-hosseini, H. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1388–1393. [Google Scholar] [CrossRef]
- Hansen, S. Translational friction coefficients for cylinders of arbitrary axial ratios estimated by Monte Carlo simulation. J. Chem. Phys. 2004, 121, 9111–9115. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905. [Google Scholar] [CrossRef]
- Amirjalayer, S.; Tafipolsky, M.; Schmid, R. Molecular Dynamics Simulation of Benzene Diffusion in MOF-5: Importance of Lattice Dynamics. Angew. Chem. Int. Ed. 2007, 46, 463–466. [Google Scholar] [CrossRef] [PubMed]
- Food and Drug Administration (FDA), Centre for Drug Evaluation and Research (CDER). Guidance for Industry Guidance for Industry Dissolution Testing of Immediate; Food and Drug Administration: Silver Spring, MD, USA, 1997; Volume 4, pp. 15–22.
- Nurhikmah, W.; Sumirtapura, Y.C.; Pamudji, J.S. Dissolution profile of mefenamic acid solid dosage forms in two compendial and biorelevant (FaSSIF) media. Sci. Pharm. 2016, 84, 181–190. [Google Scholar] [CrossRef] [PubMed]
- Yassin, S.; Goodwin, D.J.; Anderson, A.; Sibik, J.; Wilson, D.I.; Gladden, L.F.; Zeitler, J.A. The Disintegration Process in Microcrystalline Cellulose Based Tablets, Part 1: Influence of Temperature, Porosity and Superdisintegrants. J. Pharm. Sci. 2015, 104, 3440–3450. [Google Scholar] [CrossRef] [PubMed]
- Bi, Y.X.; Sunada, H.; Yonezawa, Y.; Danjo, K. Evaluation of rapidly disintegrating tablets prepared by a direct compression method. Drug Dev. Ind. Pharm. 1999, 25, 571–581. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Augsburger, L.L. The influence of swelling capacity of superdisintegrants in different pH media on the dissolution of hydrochlorothiazide from directly compressed tablets. AAPS PharmSciTech 2005, 6, 120–126. [Google Scholar] [CrossRef] [PubMed]
- Zhao, N.; Augsburger, L.L. The influence of granulation on super disintegrant performance. Pharm. Dev. Technol. 2006, 11, 47–53. [Google Scholar] [CrossRef] [PubMed]
- Gould, P.L.; Tan, S. Bin The effect of recompression on the dissolution of wet massed tablets containing “super” disintegrants. Drug Dev. Ind. Pharm. 1986, 12, 1929–1945. [Google Scholar] [CrossRef]
- García-Armenta, E.; Téllez-Medina, D.I.; Alamilla-Beltrán, L.; Arana-Errasquín, R.; Hernández-Sánchez, H.; Gutiérrez-López, G.F. Multifractal breakage patterns of thick maltodextrin agglomerates. Powder Technol. 2014, 266, 440–446. [Google Scholar] [CrossRef]
- Yap, S.F.; Adams, M.J.; Seville, J.P.K.; Zhang, Z. Single and bulk compression of pharmaceutical excipients: Evaluation of mechanical properties. Powder Technol. 2008, 185, 1–10. [Google Scholar] [CrossRef]
- Duberg, M.; Nyström, C. Studies on direct compression of tablets XVII. Porosity—pressure curves for the characterization of volume reduction mechanisms in powder compression. Powder Technol. 1986, 46, 67–75. [Google Scholar] [CrossRef]







| Formulation Composition | True Density (g/cm3) | Formulation | |||
|---|---|---|---|---|---|
| mg | %, w/w | ||||
| Granular composition | |||||
| Mefenamic acid | 1.2554 | 250.0 | 50.0 | ||
| d-mannitol | 1.4888 | 165.0 | 33.0 | ||
| Microcrystalline cellulose | 1.5701 | 50.0 | 10.0 | ||
| Croscarmellose sodium | 1.5757 | 10.0 | 2.0 | ||
| Hydroxypropyl cellulose | 1.2334 | 15.0 | 3.0 | ||
| Granulate | - | 490.0 | 98.0 | ||
| External phase composition | |||||
| Croscarmellose sodium | 1.5757 | 5.0 | 1.0 | ||
| Magnesium stearate | 1.0539 | 5.0 | 1.0 | ||
| Tablet weight | - | 500.0 | - | ||
| Tablet Parameters (N = 9) | - | A1 * | A2 | A3 | A4 |
| Tablet porosity (%, v/v) | - | 6 | 9 | 14 | 23 |
| Compressive stress (MPa) | - | 210 | 150 | 99 | 45 |
| Component | True Density (g/cm3) | Type Identifier | Component Code | C1 Constant * | C2 Constant |
|---|---|---|---|---|---|
| Mefenamic acid | 1.2554 | 1 | API | 22,082 | Not used in simulation algorithm for types 1–9 |
| d-Mannitol | 1.4888 | 10 | Non swelling, soluble filler | 200 | Not used in simulation algorithm for types 10–19 |
| Microcrystalline cellulose | 1.5701 | 31 | Non-swelling or negligible swelling, insoluble fillers | insoluble | Not used in simulation algorithm for types 30–39 |
| Croscarmellose sodium | 1.5757 | 61 | Fibrous disintegrant | insoluble | 2 ** |
| Hydroxypropyl cellulose | 1.2334 | 41 | Hydrophilic swelling matrix | 1 × 108 | Swelling of hydrophilic matrix components (types 40–49) was not included into this simulation algorithm |
| Magnesium stearate | 1.0539 | 71 | Hydrophobic ingredient | insoluble | Not used in simulation algorithm for types 70–79 |
| Formulation | Resultant Compressive Stress (MPa) | Tensile Strength (MPa) (n = 3) | Disintegration Time (s) (n = 6) | Porosity (%, v/v) |
|---|---|---|---|---|
| A1 | 210 | 3.31 ± 0.13 | 543 ± 37 | 5.6 |
| A2 | 150 | 2.53 ± 0.06 | 311 ± 16 | 9.5 |
| A3 | 99 | 1.48 ± 0.04 | 160 ± 4 | 13.7 |
| A4 | 45 | 4.72 ± 0.01 | 53 ± 2 | 23.1 |
| Source of Variance | F-Value | p-Value | Tabulated F-Value |
|---|---|---|---|
| Dissolution rates at 10 min | 31.19322 | 2.18 × 10−09 * | 2.75871 |
| Dissolution rates at 15 min | 7.89681 | 2.93 × 10−04 * | 2.75871 |
| Dissolution rates at 30 min | 26.35112 | 1.20 × 10−08 * | 2.75871 |
| Formulation | A1 | A2 | A3 | A4 | Uncompacted Granules |
|---|---|---|---|---|---|
| A1 | - | 61 | 45 | 48 | 48 |
| A2 | 61 | - | 57 | 60 | 56 |
| A3 | 45 | 57 | - | 67 | 55 |
| A4 | 48 | 60 | 67 | - | 73 |
| Uncompacted granules | 48 | 56 | 55 | 73 | - |
| Tablet | A1 | A2 | A3 | A4 | |
|---|---|---|---|---|---|
| Similarity factor (f2) | X-ray reconstructed matrices | NA * | 54 | 72 | NA * |
| Algorithmically created matrices | 67 | 68 | 73 | 71 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokoyama, R.; Kimura, G.; Schlepütz, C.M.; Huwyler, J.; Puchkov, M. Modeling of Disintegration and Dissolution Behavior of Mefenamic Acid Formulation Using Numeric Solution of Noyes-Whitney Equation with Cellular Automata on Microtomographic and Algorithmically Generated Surfaces. Pharmaceutics 2018, 10, 259. https://doi.org/10.3390/pharmaceutics10040259
Yokoyama R, Kimura G, Schlepütz CM, Huwyler J, Puchkov M. Modeling of Disintegration and Dissolution Behavior of Mefenamic Acid Formulation Using Numeric Solution of Noyes-Whitney Equation with Cellular Automata on Microtomographic and Algorithmically Generated Surfaces. Pharmaceutics. 2018; 10(4):259. https://doi.org/10.3390/pharmaceutics10040259
Chicago/Turabian StyleYokoyama, Reiji, Go Kimura, Christian M. Schlepütz, Jörg Huwyler, and Maxim Puchkov. 2018. "Modeling of Disintegration and Dissolution Behavior of Mefenamic Acid Formulation Using Numeric Solution of Noyes-Whitney Equation with Cellular Automata on Microtomographic and Algorithmically Generated Surfaces" Pharmaceutics 10, no. 4: 259. https://doi.org/10.3390/pharmaceutics10040259