Successive Short- and Long-Range Magnetic Ordering in Ba2Mn3(SeO3)6 with Honeycomb Layers of Mn3+ Ions Alternating with Triangular Layers of Mn2+ Ions
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Magnetic Susceptibility
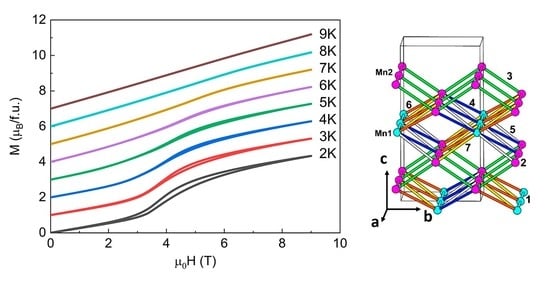
3.2. Field Dependence of Magnetization
3.3. Heat Capacity
3.4. Spin Exchanges and Interpretation
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Greedan, J.E. Geometrically frustrated magnetic materials. J. Mater. Chem. 2001, 11, 37–53. [Google Scholar] [CrossRef]
- Xiang, H.; Lee, C.; Koo, H.-J.; Gong, X.; Whangbo, M.-H. Magnetic properties and energy-mapping analysis. Dalton Trans. 2013, 42, 823–853. [Google Scholar] [CrossRef] [PubMed]
- Whangbo, M.-H.; Xiang, H.J. Magnetic properties from the perspectives of electronic Hamiltonian: Spin exchange parameters, spin orientation and spin-half misconception. In Handbook in Solid State Chemistry, Volume 5: Theoretical Descriptions; Dronskowski, R., Kikkawa, S., Stein, A., Eds.; Wiley: New York, NY, USA, 2017; pp. 285–343. [Google Scholar]
- Whangbo, M.-H.; Koo, H.-J.; Kremer, R.K. Spin exchanges between transition metal ions governed by the ligand p-orbitals in their magnetic orbitals. Molecules 2021, 26, 531. [Google Scholar] [CrossRef] [PubMed]
- Xiang, H.J.; Whangbo, M.-H. Density functional characterization of the multiferroicity in spin spiral chain cuprates. Phys. Rev. Lett. 2007, 99, 257253. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boidi, N.A.; Helman, C.; Nunez-Fernandez, Y.; Hallberg, K.; Aligia, A.A. Determination of superexchange interactions for the CuO2 chains in LiCu2O2. Phys. Rev. B 2023, 107, 085128. [Google Scholar] [CrossRef]
- Isobe, M.; Ueda, Y. Magnetic susceptibility of quasi-one-dimensional compound α′-NaV2O5—Possible spin-Peierls compound with high critical temperature of 34 K. J. Phys. Soc. Jpn. 1996, 65, 1178–1181. [Google Scholar] [CrossRef]
- Zhang, W.; Cui, M.; Tian, J.; Jiang, P.; Qian, G.; Lu, X. Two magnetic orderings and a spin-flop transition in mixed valence compound Mn3O(SeO3)3. Materials 2022, 15, 5773. [Google Scholar] [CrossRef] [PubMed]
- Ishiwata, S.; Bos, J.W.G.; Huang, Q.; Cava, R.J. Structure and magnetic properties of hollandite Ba1.2Mn8O16. J. Phys. Condens. Matter 2006, 18, 3745–3752. [Google Scholar] [CrossRef]
- Johnston, M.G.; Harrison, W.T.A. Two new octahedral/pyramidal frameworks containing both cation channels and lone-pair channels: Syntheses and structures of Ba2MnIIMn2III(SeO3)6 and PbFe2(SeO3)4. J. Sol. St. Chem. 2004, 177, 4680–4686. [Google Scholar] [CrossRef]
- Koo, H.-J.; Kremer, R.; Whangbo, M.-H. Unusual spin exchanges mediated by the molecular anion P2S64-: Theoretical analyses of the magnetic ground states, magnetic anisotropy and spin exchanges of MPS3 (M = Mn, Fe, Co, Ni). Molecules 2021, 26, 1410. [Google Scholar] [CrossRef] [PubMed]
- Zener, C. Interaction between the d-shells in the transition metals. II. Ferromagnetic compounds of manganese with perovskite structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Bain, G.A.; Berry, J.F. Diamagnetic corrections and Pascal’s constants. J. Chem Educ. 2008, 85, 532–536. [Google Scholar] [CrossRef]
- Blundell, S. Magnetism in Condenced Matter; Oxford University Press: Oxford, UK, 2001; 272p. [Google Scholar]
- Markina, M.; Vasilchikova, T.; Kuznetsova, E.; Berdonosov, P.; Olenev, A.; Chung, S.H.; Koo, H.-J.; Whangbo, M.-H.; Vasiliev, A. Preparation and characterization of francisite solid solutions Cu3Bi(Se1–xTexO3)2O2Br (x = 0–1): Possibility for francisites as starting materials for oxide van der Waals Ferromagnets. Chem. Mater. 2023, 35, 511–520. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Lee, K.H.; Lee, J.Y.; Lee, C.; Whangbo, M.-H. Evaluating the Curie-Weiss temperature of a magnetic system composed of nonequivalent magnetic ions in terms of spin exchange constants. Bull. Korean Chem. Soc. 2014, 35, 1277–1278. [Google Scholar] [CrossRef] [Green Version]
- Smart, S.J. Effective Field Theory of Magnetism; Saunders: Philadelphia, PA, USA, 1966. [Google Scholar]
- Vasiliev, A.; Volkova, O.; Zvereva, E.; Markina, M. Milestones of low-D quantum magnetism. NPJ Quant. Mater. 2018, 3, 18. [Google Scholar] [CrossRef] [Green Version]
- Lu, C.; Zhang, Y.; Cui, M.; Zhao, Z.; He, Z. Synthesis and Magnetic Properties of Two Mixed-Valence Compounds a 2MnIIMn2III(SeO3)6 (A = Sr and Ba). SSRN. Available online: https://ssrn.com/abstract=4355499 (accessed on 12 February 2023).







| Ordered Spin States | Ueff = 3 eV | Ueff = 4 eV |
|---|---|---|
| AF1 | 10.01 | 8.27 |
| AF2 | 8.80 | 7.20 |
| AF3 | 6.40 | 5.32 |
| AF4 | 8.49 | 7.81 |
| AF5 | 17.84 | 15.03 |
| AF6 | 13.26 | 12.68 |
| AF7 | 3.62 | 3.29 |
| AF8 | 0 | 0 |
| Path | Geometrical Parameters | Spin Exchanges (in K) | ||
|---|---|---|---|---|
| Ions Involved | Distance, Å | Ueff = 3 eV | Ueff = 4 eV | |
| J1 | Mn1…Mn1 | 5.4717 | −2.23 | −1.74 |
| J2 | Mn2…Mn2 | 5.4717 | −2.62 | −2.14 |
| J3 | Mn2…Mn2 | 5.4655 | 1.51 | 1.80 |
| J4 | Mn1…Mn2 | 5.9554 | −2.38 | −1.63 |
| J5 | Mn1…Mn2 | 6.0883 | −0.88 | −0.45 |
| J6 | Mn1…Mn2 | 5.9737 | −2.05 | −1.43 |
| J7 | Mn1…Mn2 | 6.1063 | 3.88 | 3.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moskin, A.; Kozlyakova, E.; Chung, S.H.; Koo, H.-J.; Whangbo, M.-H.; Vasiliev, A. Successive Short- and Long-Range Magnetic Ordering in Ba2Mn3(SeO3)6 with Honeycomb Layers of Mn3+ Ions Alternating with Triangular Layers of Mn2+ Ions. Materials 2023, 16, 2685. https://doi.org/10.3390/ma16072685
Moskin A, Kozlyakova E, Chung SH, Koo H-J, Whangbo M-H, Vasiliev A. Successive Short- and Long-Range Magnetic Ordering in Ba2Mn3(SeO3)6 with Honeycomb Layers of Mn3+ Ions Alternating with Triangular Layers of Mn2+ Ions. Materials. 2023; 16(7):2685. https://doi.org/10.3390/ma16072685
Chicago/Turabian StyleMoskin, Artem, Ekaterina Kozlyakova, Seung Hwan Chung, Hyun-Joo Koo, Myung-Hwan Whangbo, and Alexander Vasiliev. 2023. "Successive Short- and Long-Range Magnetic Ordering in Ba2Mn3(SeO3)6 with Honeycomb Layers of Mn3+ Ions Alternating with Triangular Layers of Mn2+ Ions" Materials 16, no. 7: 2685. https://doi.org/10.3390/ma16072685