Adjusting the Single-Diode Model Parameters of a Photovoltaic Module with Irradiance and Temperature
Abstract
:1. Introduction
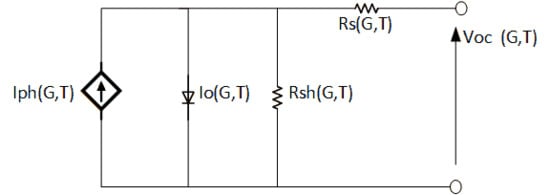
2. Mathematical Analysis of the Single-Diode Model
3. Method of Adjusting the SDM Model Parameters
3.1. Short-Circuit Current
3.1.1. Method 1
3.1.2. Method 2
3.2. Open-Circuit Voltage
3.2.1. Method 1
3.2.2. Method 2
3.2.3. Method 3
3.2.4. Method 4
3.2.5. Method 5
3.3. Photocurrent
3.3.1. Method 1
3.3.2. Method 2
3.3.3. Method 3
3.3.4. Method 4
3.4. Ideality Factor n
3.5. Saturation Current
3.5.1. Method 1
3.5.2. Method 2
3.5.3. Method 3
3.5.4. Method 4
3.5.5. Method 5
3.6. Series and Shunt Resistances
3.6.1. Method 1
3.6.2. Method 2
3.6.3. Method 3
3.6.4. Method 4
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiao, W.; Dunford, W.G.; Capel, A. A novel modeling method for photovoltaic cells. In Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 1950–1956. [Google Scholar]
- Bellini, A.; Bifaretti, S.; Iacovone, V.; Cornaro, C. “Simplified Model of a Photovoltaic Module,” in Applied Electronics; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Villalva, M.; Gazoli, J.R.; Filho, E. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays. IEEE Trans. Power Electron. 2009, 24, 1198–1208. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Power Electronics and Control Techniques for Maximum Energy Harvesting in Photovoltaic Systems; Informa UK Limited: Colchester, UK, 2017. [Google Scholar]
- Huang, P.-H.; Xiao, W.; Peng, J.C.-H.; Kirtley, J.L. Comprehensive Parameterization of Solar Cell: Improved Accuracy with Simulation Efficiency. IEEE Trans. Ind. Electron. 2015, 63, 1549–1560. [Google Scholar] [CrossRef]
- Mahmoud, Y.; El-Saadany, E.F. A Photovoltaic Model with Reduced Computational Time. IEEE Trans. Ind. Electron. 2014, 62, 1. [Google Scholar] [CrossRef]
- Tolić, I.; Primorac, M.; Milicevic, K. Measurement Uncertainty Propagation through Basic Photovoltaic Cell Models. Energies 2019, 12, 1029. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Evaluation of Analytical Methods for Parameter Extraction of PV modules. Energy Procedia 2017, 134, 69–78. [Google Scholar] [CrossRef]
- Chegaar, M.; Hamzaoui, A.; Namoda, A.; Petit, P.; Aillerie, M.; Herguth, A. Effect of Illumination Intensity on Solar Cells Parameters. Energy Procedia 2013, 36, 722–729. [Google Scholar] [CrossRef]
- Singh, P.; Ravindra, N. Temperature dependence of solar cell performance—An analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- Anani, N.; Shahid, M.; Al-Kharji, O.; Ponciano, J. A CAD Package for Modeling and Simulation of PV Arrays under Partial Shading Conditions. Energy Procedia 2013, 42, 397–405. [Google Scholar] [CrossRef] [Green Version]
- Silvestre, S.; Boronat, A.; Chouder, A. Study of bypass diodes configuration on PV modules. Appl. Energy 2009, 86, 1632–1640. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Variation of the performance of a PV panel with the number of bypass diodes and partial shading patterns. In Proceedings of the 2019 International Conference on Power Generation Systems and Renewable Energy Technologies (PGSRET), Istanbul, Turkey, 26–27 August 2019; pp. 1–4. [Google Scholar]
- Ibrahim, H.; Anani, N. Study of the effect of different configurations of bypass diodes on the performance of a PV string. In Human Centred Intelligent Systems; Springer: Berlin, Germany, 2019; pp. 593–600. [Google Scholar]
- Brano, V.L.; Orioli, A.; Ciulla, G.; Di Gangi, A. An improved five-parameter model for photovoltaic modules. Sol. Energy Mater. Sol. Cells 2010, 94, 1358–1370. [Google Scholar] [CrossRef]
- Chatterjee, A.; Keyhani, A.; Kapoor, D. Identification of Photovoltaic Source Models. IEEE Trans. Energy Convers. 2011, 26, 883–889. [Google Scholar] [CrossRef]
- Sera, D.; Teodorescu, R.; Rodriguez, P. Photovoltaic module diagnostics by series resistance monitoring and temperature and rated power estimation. In Proceedings of the 2008 34th Annual Conference of IEEE Industrial Electronics, Orlando, FL, USA, 10–13 November 2008; pp. 2195–2199. [Google Scholar]
- Skoplaki, E.; Palyvos, J. On the temperature dependence of photovoltaic module electrical performance: A review of efficiency/power correlations. Sol. Energy 2009, 83, 614–624. [Google Scholar] [CrossRef]
- Ibrahim, H.; Anani, N. Variations of PV module parameters with irradiance and temperature. Energy Procedia 2017, 134, 276–285. [Google Scholar] [CrossRef]
- Kennerud, K. Analysis of Performance Degradation in CdS Solar Cells. In IEEE Trans. Aerosp. Electron. Syst. 1969, 5, 912–917. [Google Scholar] [CrossRef]
- Siddique, H.A.B.; Xu, P.; De Doncker, R.W. Parameter extraction algorithm for one-diode model of PV panels based on datasheet values. In Proceedings of the 2013 International Conference on Clean Electrical Power (ICCEP), Alghero, Italy, 11–13 June 2013; pp. 7–13. [Google Scholar]
- Cubas, J.; Pindado, S.; Victoria, M. On the analytical approach for modeling photovoltaic systems behavior. J. Power Sources 2014, 247, 467–474. [Google Scholar] [CrossRef] [Green Version]
- Dongue, S.B.; Njomo, D.; Ebengai, L. An Improved Nonlinear Five-Point Model for Photovoltaic Modules. Int. J. Photoenergy 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Ghani, F.; Duke, M. Numerical determination of parasitic resistances of a solar cell using the Lambert W-function. Sol. Energy 2011, 85, 2386–2394. [Google Scholar] [CrossRef]
- Louzazni, M.; Khouya, A.; Crăciunescu, A.; Amechnoue, K.; Mussetta, M. Modelling and Parameters Extraction of Flexible Amorphous Silicon Solar Cell a-Si:H. Appl. Sol. Energy 2020, 56, 1–12. [Google Scholar] [CrossRef]
- Luo, X.; Cao, L.; Wang, L.; Zhao, Z.; Huang, C. Parameter identification of the photovoltaic cell model with a hybrid Jaya-NM algorithm. Optik 2018, 171, 200–203. [Google Scholar] [CrossRef]
- Saloux, E.; Teyssedou, A.; Sorin, M. Explicit model of photovoltaic panels to determine voltages and currents at the maximum power point. Sol. Energy 2011, 85, 713–722. [Google Scholar] [CrossRef]
- Carrero, C.; Ramirez, D.; Rodriguez, J.; Platero, C. Accurate and fast convergence method for parameter estimation of PV generators based on three main points of the I–V curve. Renew. Energy 2011, 36, 2972–2977. [Google Scholar] [CrossRef]
- Khezzar, R.; Zereg, M.; Khezzar, A. Modeling improvement of the four parameter model for photovoltaic modules. Sol. Energy 2014, 110, 452–462. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, H.; Fang, Z. A novel model for photovoltaic array performance prediction. Appl. Energy 2007, 84, 1187–1198. [Google Scholar] [CrossRef]
- De Soto, W.; Klein, S.; Beckman, W. Improvement and validation of a model for photovoltaic array performance. Sol. Energy 2006, 80, 78–88. [Google Scholar] [CrossRef]
- Mahmoud, Y.; Xiao, W.; Zeineldin, H.H. A Parameterization Approach for Enhancing PV Model Accuracy. IEEE Trans. Ind. Electron. 2012, 60, 5708–5716. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. A procedure to calculate the five-parameter model of crystalline silicon photovoltaic modules on the basis of the tabular performance data. Appl. Energy 2013, 102, 1160–1177. [Google Scholar] [CrossRef]
- da Luz, C.M.A.; Tofoli, F.L.; Vicente, P.D.S.; Vicente, E.M. Assessment of the ideality factor on the performance of photovoltaic modules. Energy Convers. Manag. 2018, 167, 63–69. [Google Scholar] [CrossRef]
- Kim, W.; Choi, W. A novel parameter extraction method for the one-diode solar cell model. Sol. Energy 2010, 84, 1008–1019. [Google Scholar] [CrossRef]
- Islam, M.H.; Djokic, S.Z.; Desmet, J.; Verhelst, B. Measurement-based modelling and validation of PV systems. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Can, H.; Ickilli, D.; Parlak, K. A New Numerical Solution Approach for the Real-Time Modeling of Photovoltaic Panels. In Proceedings of the 2012 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar]
- Bai, J.; Liu, S.; Hao, Y.; Zhang, Z.; Jiang, M.; Zhang, Y. Development of a new compound method to extract the five parameters of PV modules. Energy Convers. Manag. 2014, 79, 294–303. [Google Scholar] [CrossRef]
- Ghani, F.; Duke, M.; Carson, J. Numerical calculation of series and shunt resistance of a photovoltaic cell using the Lambert W-function: Experimental evaluation. Sol. Energy 2013, 87, 246–253. [Google Scholar] [CrossRef]
- Mahmoud, Y.; Xiao, W.; Zeineldin, H.H. A Simple Approach to Modeling and Simulation of Photovoltaic Modules. IEEE Trans. Sustain. Energy 2012, 3, 185–186. [Google Scholar] [CrossRef]
- Ma, J.; Man, K.L.; Ting, T.; Zhang, N.; Lim, E.G.; Guan, S.-U.; Wong, P.W.; Krilavičius, T.; Saulevicius, D.; Lei, C.-U. Simple Computational Method of Predicting Electrical Characteristics in Solar Cells. Elektron. Elektrotechnika 2014, 20, 41–44. [Google Scholar] [CrossRef] [Green Version]
- Virtuani, A.; Lotter, E.; Powalla, M. Performance of Cu(In,Ga)Se2 solar cells under low irradiance. Thin Solid Films 2003, 431, 443–447. [Google Scholar] [CrossRef]
- POSHARP Inc. Shell SQ 150-PC Solar Panel from Shell Solar. Available online: http://www.posharp.com/shell-sq-150-pc-solar-panel-from-shell-solar_p1838324422d.aspx (accessed on 10 January 2020).
- KYOCERA North America. KC 175 GT. Available online: https://search.kyocera.co.jp/search?site=ZHS4H5NP&charset=UTF-8&group=62&design=69&query=KC175GT&_ga=2.256746382.462656309.1590188877-1511522101.1586353898 (accessed on 10 March 2020).
- POSHARP Inc. ST40 Solar Panel. Available online: http://www.posharp.com/st-40-solar-panel-from-shell-solar_p1208198951d.aspx (accessed on 1 May 2020).

| Parameters | Shell SQ150 | KC175GT | Shell ST40 |
|---|---|---|---|
| −161 × 10−3 | −1.09 × 10−1 | −100 × 10−3 | |
| 1.4 × 10−3 | 3.18 × 10−3 | 0.35 × 10−3 | |
| 72 | 84 | 36 |
| Constant | α | β | γ |
|---|---|---|---|
| Shell SQ150 | 0.998 | 0.055 | 1.0797 |
| KC175GT | 0.977 | 0.053 | 1.32 |
| Shell ST40 | 0.996 | 0.085 | 1.367 |
| Parameters | Shell SQ150 | KC175GT | Shell ST40 |
|---|---|---|---|
| 1.4226 Ω | |||
| 952.405 Ω | |||
| 4.8024 A | 8.0926 A | 2.684 A |
| PV Module | Irradiance W/m2 | |||||
|---|---|---|---|---|---|---|
| 1000 | 800 | 600 | 400 | 200 | ||
| Measured | 8.09 | 6.80889 | 4.91094 | 3.27396 | 1.56581 | |
| KC175GT | Method 1 | 8.09 | 6.472 | 4.854 | 3.236 | 1.618 |
| %error | 4.95478 | 1.1595 | 1.1595 | 3.331 | ||
| Method 2 | 8.09 | 6.5053 | 4.9114 | 3.3049 | 1.679 | |
| %error | 4.4587 | 0.0094 | 0.945 | 7.23 | ||
| Measured | 4.8 | 3.84 | 2.88 | 1.90884 | 0.94884 | |
| SQ150 | Method 1 | 4.8 | 3.84 | 2.88 | 1.92 | 0.96 |
| %error | 0 | 0 | 0.5847 | 1.1762 | ||
| Method 2 | 4.8 | 3.8417 | 2.8829 | 1.9235 | 0.9631 | |
| %error | 0.0443 | 0.1007 | 0.768 | 1.5029 | ||
| Measured | 2.68 | 2.14894 | 1.61171 | 1.07447 | 0.53724 | |
| ST40 | Method 1 | 2.68 | 2.144 | 1.608 | 1.072 | 0.536 |
| %error | 0.2299 | 0.2302 | 0.2299 | 0.2301 | ||
| Method 2 | 2.68 | 2.1459 | 1.6113 | 1.0759 | 0.539 | |
| %error | 0.1415 | 0.0254 | 0.1331 | 0.4207 | ||
| PV Modules | Equation (30) | Method 1 | Method 2 | Method 3 | Method 4 |
|---|---|---|---|---|---|
| KC175GT | 8.0926406 | 8.09 | 8.09263991 | 8.09264031 | 8.0926406 |
| SQ150 | 4.8024316 | 4.8 | 4.80243089 | 4.80243114 | 4.80243165 |
| ST40 | 2.6840051 | 2.68 | 2.6840031 | 2.68400152 | 2.68400513 |
| G (W/m2) | Measured | Method 1 | Method 2 | Method 3 | Method 4 | Method 5 |
|---|---|---|---|---|---|---|
| 1000 | 43.4 | 43.4 | 43.4 | 43.4 | 43.4 | 43.4 |
| %error | 0 | 0 | 0 | 0 | 0 | |
| 800 | 42.91547 | 43.4 | 42.823523 | 42.80548 | 43.38809 | 42.87381 |
| %error | 1.1165 | 0.2143 | 0.2563 | 1.1013 | 0.0971 | |
| 600 | 42.22329 | 43.4 | 42.05706 | 42.03902 | 43.37352 | 42.21398 |
| %error | 2.7869 | 0.3937 | 0.4364 | 2.7242 | 0.0221 | |
| 400 | 41.25423 | 43.4 | 40.97679 | 40.95875 | 43.35267 | 41.31775 |
| %error | 5.2013 | 0.6725 | 0.7164 | 5.0866 | 0.154 | |
| 200 | 39.59298 | 43.4 | 39.13005 | 39.11201 | 43.32139 | 39.87068 |
| %error | 8.7719 | 1.1692 | 1.2148 | 9.4169 | 0.70139 |
| Irradiance | ||||||
|---|---|---|---|---|---|---|
| (W/m2) | Measured | Method 1 | Method 2 | Method 3 | Method 4 | Method 5 |
| 1000 | 29.2 | 29.2 | 29.2 | 29.2 | 29.2 | 29.2 |
| %error | 0 | 0 | 0 | 0 | 0 | |
| 800 | 28.81579 | 29.2 | 28.80708 | 28.78606 | 29.18809 | 28.8587 |
| %error | 1.365 | 0.03023 | 0.1032 | 1.292 | 0.1489 | |
| 600 | 28.43158 | 29.2 | 28.27343 | 28.25241 | 29.17352 | 28.43029 |
| %error | 2.7027 | 0.5563 | 0.6302 | 2.6096 | 0.4554 | |
| 400 | 27.81684 | 29.2 | 27.52128 | 27.50026 | 29.15432 | 27.8476 |
| %error | 4.9724 | 1.0625 | 1.1381 | 4.8082 | 0.1107 | |
| 200 | 27.04842 | 29.2 | 26.23548 | 26.21446 | 29.12429 | 26.905 |
| %error | 7.9546 | 3.0055 | 3.0832 | 7.6763 | 0.5302 | |
| Irradiance | ||||||
|---|---|---|---|---|---|---|
| (W/m2) | Measured | Method 1 | Method 2 | Method 3 | Method 4 | Method 5 |
| 1000 | 23.3 | 23.3 | 23.3 | 23.3 | 23.3 | 23.3 |
| %error | 0 | 0 | 0 | 0 | 0 | |
| 800 | 22.79815 | 23.3 | 22.99962 | 22.98971 | 23.28809 | 22.86629 |
| %error | 2.2013 | 0.8837 | 0.8402 | 2.149 | 0.2989 | |
| 600 | 22.29631 | 23.3 | 22.59959 | 22.58968 | 23.27352 | 22.33041 |
| %error | 4.5016 | 1.3602 | 1.3158 | 4.3828 | 0.1529 | |
| 400 | 21.54354 | 23.3 | 22.03578 | 22.02587 | 23.25432 | 21.61641 |
| %error | 8.1531 | 2.2849 | 2.2389 | 7.941 | 0.3383 | |
| 200 | 20.21723 | 23.3 | 21.07194 | 21.06204 | 23.22429 | 20.49609 |
| %error | 15.248 | 4.2276 | 4.1787 | 14.8738 | 1.3793 | |
| Temperature | |||||
|---|---|---|---|---|---|
| (°C) | Measured | Method 1 | %Error | Method 5 | %Error |
| 20 | 44.205 | 44.205 | 0 | 44.2002 | 0.0109 |
| 25 | 43.4 | 43.4 | 0 | 43.4 | 0 |
| 30 | 42.7315 | 43.3195 | 1.376 | 42.6273 | 0.2439 |
| 40 | 41.258 | 40.985 | 0.6617 | 41.1587 | 0.2407 |
| 50 | 39.7845 | 39.375 | 1.0218 | 39.7846 | 0.00025 |
| 60 | 38.311 | 37.765 | 1.4252 | 38.4962 | 0.4834 |
| Temperature | |||||
|---|---|---|---|---|---|
| (°C) | Measured | Method 1 | %Error | Method 5 | %Error |
| 25 | 29.2 | 29.2 | 0 | 29.2 | 0 |
| 50 | 26.26533 | 26.475 | 0.7983 | 26.2649 | 0.00164 |
| 75 | 23.25729 | 23.75 | 2.1185 | 23.8122 | 2.386 |
| Temperature | |||||
|---|---|---|---|---|---|
| (°C) | Measured | Method 1 | %Error | Method 5 | %Error |
| 20 | 23.8 | 23.8 | 0 | 23.8452 | 0.1899 |
| 25 | 23.3 | 23.3 | 0 | 23.3 | 0 |
| 30 | 22.81138 | 22.8 | 0.04989 | 22.776 | 0.1551 |
| 40 | 21.85938 | 21.8 | 0.2716 | 21.7872 | 0.3302 |
| 50 | 20.87077 | 20.8 | 0.3391 | 20.8703 | 0.0023 |
| 60 | 19.91877 | 19.8 | 0.5963 | 20.0184 | 0.5002 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anani, N.; Ibrahim, H. Adjusting the Single-Diode Model Parameters of a Photovoltaic Module with Irradiance and Temperature. Energies 2020, 13, 3226. https://doi.org/10.3390/en13123226
Anani N, Ibrahim H. Adjusting the Single-Diode Model Parameters of a Photovoltaic Module with Irradiance and Temperature. Energies. 2020; 13(12):3226. https://doi.org/10.3390/en13123226
Chicago/Turabian StyleAnani, Nader, and Haider Ibrahim. 2020. "Adjusting the Single-Diode Model Parameters of a Photovoltaic Module with Irradiance and Temperature" Energies 13, no. 12: 3226. https://doi.org/10.3390/en13123226