Three for the Price of One: Concomitant I⋯N, I⋯O, and I⋯π Halogen Bonds in the Same Crystal Structure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis and Crystallization
2.2. Computational Details
3. Results
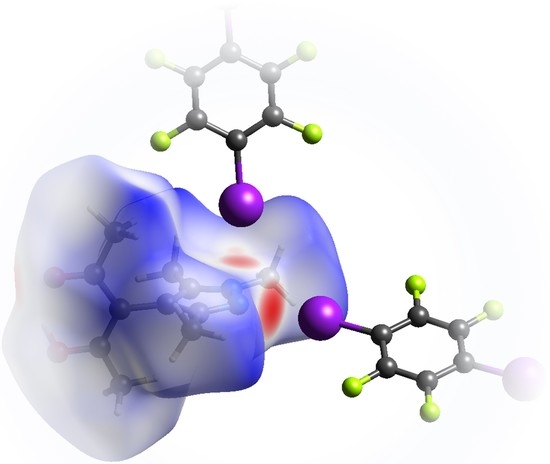
3.1. Structural Features of 1
- A
- The pyrazole N⋯I halogen bond occurs between the TFDIB moiety located on Wyckoff position and N1 at a N⋯I distance of 2.909(4) Å. For sufficiently precise data, anti-correlation between short I⋯donor XBs and long C–I bonds was reported [41]. Our data for 1 meets these requirements and allow us to discuss the competing XBs in the light of their associated C–I bonds. We found that C13–I1 is elongated and 0.02 Å is longer than the corresponding bond in pure TFDIB (CSD refcode ZZZAVM02 [42]). Only two contacts between a pyrazole and TFDIB were documented in the CSD; they amount to 2.860 Å in TOJBIE [43] and 2.934 Å in TIPKAH (In refcodes TIPKAH and AWUWOH, not p-TFDIB, but o-TFDIB was used) [44].
- B
- Another short contact exists between the acetylacetone keto O1 and I2 of the second TFDIB moiety, occupying the positions close to the inversion center with Wyckoff letter ; it amounts to 2.929(3) Å. As expected, the C–I bond in this moiety is less elongated than the C–I bond in the I⋯N halogen bond A. This is due to the weaker basicity of oxygen compared to the iminic nitrogen of the pyrazole moiety. For similar motifs, such as pyridyl substituted β-diketones, I⋯Oketo amounts to about 3.05 Å (refcodes TAXYID [45], AWUWOH‡ [46]). In all cases of protonated β-diketones, the halogen bond acceptor is the keto oxygen, not the enol bond acceptor. Chemical intuition suggests that the keto oxygen is associated with the more negative charge. In several cocrystals of β-diketonato complexes with TFDIB, two oxygens of different β-diketonate ligands act as halogen bond acceptors; the XB is oriented more or less symmetrically bifurcated towards the midpoint between these two oxygen atoms [47,48].
- C
- Last but not least, I3 from the third symmetry independent TFDIB moiety, located around the inversion center with Wyckoff position , acts as XB donor towards the pyrazole π-system with a distance of 3.2157(3) Å. As expected by the theoretical electrostatic potential for pyrazoles [49], the closest contact atom for I3 is the iminic N1 with a distance of 3.241(4) Å. Lewis basic π-systems as XB acceptors are known in literature, e.g., for cyclopentadienyl ligands [50], imidazoles [51], or carbazoles [52], and have been evaluated theoretically [53,54,55]; however, to the best of our knowledge, no pyrazole-π⋯I interactions with perfluoronated iodobenzenes have been reported to this date. This is also due to the competition with the more prominent I⋯N XB, as present in interaction A.
3.2. Theoretical Electron Density Considerations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCP | bond critical point |
| BPL | bond path length |
| HacacMePz | 3-(1,3,5-trimethyl-1H-4-pyrazolyl)pentane-2,4-dione |
| Pz | pyrazole |
| QTAIM | Quantum Theory of Atoms in Molecules |
| SCXRD | single-crystal X-ray diffraction |
| TFDIB | 2,3,5,6-tetrafluoro-1,4-diiodobenzene |
| XB | halogen bond |
References
- Politzer, P.; Lane, P.; Concha, M.C.; Ma, Y.; Murray, J.S. An overview of halogen bonding. J. Mol. Model. 2007, 13, 305–311. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The -hole. Proceedings of “Modeling interactions in biomolecules II”, Prague, September 5th–9th, 2005. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Aakeröy, C.B.; Panikkattu, S.; Chopade, P.D.; Desper, J. Competing hydrogen-bond and halogen-bond donors in crystal engineering. CrystEngComm 2013, 15, 3125–3136. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Hu, R.X.; Pang, X.; Gao, H.Y.; Jin, W.J. The phosphorescent co-crystals of 1,4-diiodotetrafluorobenzene and bent 3-ring-N-heterocyclic hydrocarbons by C–I⋯N and C–I⋯ halogen bonds. CrystEngComm 2014, 16, 7942–7948. [Google Scholar] [CrossRef]
- Wang, R.; Hartnick, D.; Englert, U. Short is strong: Experimental electron density in a very short N⋯I halogen bond. Z. Kristallogr.—Cryst. Mater. 2018, 233, 733–744. [Google Scholar] [CrossRef]
- Otte, F.; Kleinheider, J.; Hiller, W.; Wang, R.; Englert, U.; Strohmann, C. Weak yet Decisive: Molecular Halogen Bond and Competing Weak Interactions of Iodobenzene and Quinuclidine. J. Am. Chem. Soc. 2021, 143, 4133–4137. [Google Scholar] [CrossRef]
- Sarwar, M.G.; Dragisic, B.; Sagoo, S.; Taylor, M.S. A Tridentate Halogen-Bonding Receptor for Tight Binding of Halide Anions. Angew. Chem. Int. Ed. 2010, 122, 1718–1721. [Google Scholar] [CrossRef]
- van Terwingen, S.; Nachtigall, N.; Ebel, B.; Englert, U. N-Donor-Functionalized Acetylacetones for Heterobimetallic Coordination Polymers, the Next Episode: Trimethylpyrazoles. Cryst. Growth Des. 2021, 21, 2962–2969. [Google Scholar] [CrossRef]
- Posavec, L.; Nemec, V.; Stilinović, V.; Cinčić, D. Halogen and Hydrogen Bond Motifs in Ionic Cocrystals Derived from 3-Halopyridinium Halogenides and Perfluorinated Iodobenzenes. Cryst. Growth Des. 2021, 21, 6044–6050. [Google Scholar] [CrossRef]
- Ormond-Prout, J.E.; Smart, P.; Brammer, L. Cyanometallates as Halogen Bond Acceptors. Cryst. Growth Des. 2012, 12, 205–216. [Google Scholar] [CrossRef]
- Shen, Q.J.; Pang, X.; Zhao, X.R.; Gao, H.Y.; Sun, H.L.; Jin, W.J. Phosphorescent cocrystals constructed by 1,4-diiodotetrafluorobenzene and polyaromatic hydrocarbons based on C–I⋯ halogen bonding and other assisting weak interactions. CrystEngComm 2012, 14, 5027. [Google Scholar] [CrossRef]
- Wang, C.; Danovich, D.; Mo, Y.; Shaik, S. On The Nature of the Halogen Bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C. The halogen bond: An interim perspective. Phys. Chem. Chem. Phys. 2010, 12, 7736–7747. [Google Scholar] [CrossRef] [PubMed]
- Aakeröy, C.B.; Welideniya, D.; Desper, J. Ethynyl hydrogen bonds and iodoethynyl halogen bonds: A case of synthon mimicry. CrystEngComm 2017, 19, 11–13. [Google Scholar] [CrossRef]
- Hassel, O.; Hvoslef, J. The Structure of Bromine 1,4-Dioxonate. Acta Chim. Scand. 1954, 8, 873. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Halogen bonding: An interim discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef]
- Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The many faces of halogen bonding: A review of theoretical models and methods. Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Champness, N.R.; Janiak, C. Recent advances in crystal engineering. CrystEngComm 2010, 12, 22–43. [Google Scholar] [CrossRef]
- Priimagi, A.; Cavallo, G.; Metrangolo, P.; Resnati, G. The halogen bond in the design of functional supramolecular materials: Recent advances. Acc. Chem. Res. 2013, 46, 2686–2695. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Sušanj, R.; Nemec, V.; Bedeković, N.; Cinčić, D. Halogen Bond Motifs in Cocrystals of N,N,O and N,O,O Acceptors Derived from Diketones and Containing a Morpholine or Piperazine Moiety. Cryst. Growth Des. 2022, 22, 5135–5142. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- van Terwingen, S.; Brüx, D.; Wang, R.; Englert, U. Hydrogen-Bonded and Halogen-Bonded: Orthogonal Interactions for the Chloride Anion of a Pyrazolium Salt. Molecules 2021, 26, 3982. [Google Scholar] [CrossRef]
- Bruker. SAINT+: Program for Reduction of Data Collected on Bruker CCD Area Detector Diffractometer; Bruker AXS Inc.: Billerica, MA, USA, 2009. [Google Scholar]
- Bruker. SADABS: Program for Empirical Absorption Correction of Area Detector Data; Bruker AXS Inc.: Billerica, MA, USA, 2008. [Google Scholar]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. A 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allen, F.H.; Bruno, I.J. Bond lengths in organic and metal-organic compounds revisited: X-H bond lengths from neutron diffraction data. Acta Crystallogr. B 2010, 66, 380–386. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Account 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Easton, R.E.; Giesen, D.J.; Welch, A.; Cramer, C.J.; Truhlar, D.G. The MIDI! basis set for quantum mechanical calculations of molecular geometries and partial charges. Theor. Chim. Acta 1996, 93, 281–301. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. GAUSSIAN 16, Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Keith, T.A. AIMAll: Version 17.01.25; TK Gristmill Software: Overland Park, KS, USA, 2017. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Abramov, Y.A. On the Possibility of Kinetic Energy Density Evaluation from the Experimental Electron-Density Distribution. Acta Crystallogr. A 1997, 53, 264–272. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Espinosa, E.; Lecomte, C.; Molins, E. Experimental electron density overlapping in hydrogen bonds: Topology vs. energetics. Chem. Phys. Lett. 1999, 300, 745–748. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.J.; Grabowsky, S.; Jayatilaka, D.; Spackman, M.A. Accurate and Efficient Model Energies for Exploring Intermolecular Interactions in Molecular Crystals. J. Phys. Chem. Lett. 2014, 5, 4249–4255. [Google Scholar] [CrossRef] [Green Version]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. D 2009, 65, 148–155. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; George, J.; Potts, S.K.; Kremer, M.; Dronskowski, R.; Englert, U. The many flavours of halogen bonds—Message from experimental electron density and Raman spectroscopy. Acta Crystallogr. C 2019, 75, 1190–1201. [Google Scholar] [CrossRef] [Green Version]
- Oh, S.Y.; Nickels, C.W.; Garcia, F.; Jones, W.; Friščić, T. Switching between halogen- and hydrogen-bonding in stoichiometric variations of a cocrystal of a phosphine oxide. CrystEngComm 2012, 14, 6110. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Desper, J.; Fasulo, M.; Hussain, I.; Levin, B.; Schultheiss, N. Ten years of co-crystal synthesis; the good, the bad, and the ugly. CrystEngComm 2008, 10, 1816. [Google Scholar] [CrossRef]
- Andree, S.N.L.; Sinha, A.S.; Aakeröy, C.B. Structural Examination of Halogen-Bonded Co-Crystals of Tritopic Acceptors. Molecules 2018, 23, 163. [Google Scholar] [CrossRef]
- Brown, J.J.; Brock, A.J.; Pfrunder, M.C.; Sarju, J.P.; Perry, A.Z.; Whitwood, A.C.; Bruce, D.W.; McMurtrie, J.C.; Clegg, J.K. Co-Crystallisation of 1,4-Diiodotetrafluorobenzene with Three Different Symmetric Dipyridylacetylacetone Isomers Produces Four Halogen-Bonded Architectures. Aust. J. Chem. 2017, 70, 594. [Google Scholar] [CrossRef]
- Martinez, V.; Bedeković, N.; Stilinović, V.; Cinčić, D. Tautomeric Equilibrium of an Asymmetric beta-Diketone in Halogen-Bonded Cocrystals with Perfluorinated Iodobenzenes. Crystals 2021, 11, 699. [Google Scholar] [CrossRef]
- Stilinović, V.; Grgurić, T.; Piteša, T.; Nemec, V.; Cinčić, D. Bifurcated and Monocentric Halogen Bonds in Cocrystals of Metal(II) Acetylacetonates with p-Dihalotetrafluorobenzenes. Cryst. Growth Des. 2019, 19, 1245–1256. [Google Scholar] [CrossRef]
- Merkens, C.; Pan, F.; Englert, U. 3-(4-Pyridyl)-2,4-pentanedione—A bridge between coordinative, halogen, and hydrogen bonds. CrystEngComm 2013, 15, 8153. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Computational analysis of polyazoles and their N-oxides. Struct. Chem. 2017, 28, 1045–1063. [Google Scholar] [CrossRef]
- Torubaev, Y.V.; Skabitsky, I.V.; Raghuvanshi, A. The structural landscape of ferrocenyl polychalcogenides. J. Organomet. Chem. 2021, 951, 122006. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Wijethunga, T.K.; Desper, J. Practical crystal engineering using halogen bonding: A hierarchy based on calculated molecular electrostatic potential surfaces. J. Mol. Struct. 2014, 1072, 20–27. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, Y.J.; Gao, H.Y.; Jin, W.J. Effect of N-methyl and ethyl on phosphorescence of carbazole in cocrystals assembled by CI⋯ halogen bond, -hole⋯ bond and other interactions using 1,4-diiodotetrafluorobenzene as donor. J. Photochem. Photobiol. A Chem. 2014, 289, 31–38. [Google Scholar] [CrossRef]
- Riley, K.E.; Vazquez, M.; Umemura, C.; Miller, C.; Tran, K.A. Exploring the (Very Flat) Potential Energy Landscape of R-Br⋯ Interactions with Accurate CCSD(T) and SAPT Techniques. Chem. Eur. J. 2016, 22, 17690–17695. [Google Scholar] [CrossRef] [Green Version]
- Forni, A.; Pieraccini, S.; Rendine, S.; Gabas, F.; Sironi, M. Halogen-bonding interactions with systems: CCSD(T), MP2, and DFT calculations. ChemPhysChem 2012, 13, 4224–4234. [Google Scholar] [CrossRef]
- Wu, M.; Li, M.; Yuan, L.; Pan, F. “Useless Channels” in a Molecular Crystal Formed via F⋯F and F⋯ Halogen Bonds. Cryst. Growth Des. 2022, 22, 971–975. [Google Scholar] [CrossRef]
- O’Keeffe, M.; Peskov, M.A.; Ramsden, S.J.; Yaghi, O.M. The Reticular Chemistry Structure Resource (RCSR) database of, and symbols for, crystal nets. Acc. Chem. Res. 2008, 41, 1782–1789. [Google Scholar] [CrossRef] [PubMed]
- Macrae, C.F.; Sovago, I.; Cottrell, S.J.; Galek, P.T.A.; McCabe, P.; Pidcock, E.; Platings, M.; Shields, G.P.; Stevens, J.S.; Towler, M.; et al. Mercury 4.0: From visualization to analysis, design and prediction. J. Appl. Crystallogr. 2020, 53, 226–235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nemec, V.; Cinčić, D. The Halogen Bonding Proclivity of the sp3 Sulfur Atom as a Halogen Bond Acceptor in Cocrystals of Tetrahydro-4H-thiopyran-4-one and Its Derivatives. Cryst. Growth Des. 2022, 22, 5796–5801. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19–32. [Google Scholar] [CrossRef]
- Bianchi, R.; Forni, A.; Pilati, T. The experimental electron density distribution in the complex of (E)-1,2-bis(4-pyridyl)ethylene with 1,4-diiodotetrafluorobenzene at 90 K. Chem. Eur. J. 2003, 9, 1631–1638. [Google Scholar] [CrossRef]
- Bianchi, R.; Forni, A.; Pilati, T. Experimental electron density study of the supramolecular aggregation between 4,4’-dipyridyl-N,N’-dioxide and 1,4-diiodotetrafluorobenzene at 90 K. Acta Crystallogr. B 2004, 60, 559–568. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsov, M.L. Can halogen bond energy be reliably estimated from electron density properties at bond critical point? The case of the (A)nZ–Y⋯X– (X, Y = F, Cl, Br) interactions. Int. J. Quantum Chem. 2019, 119, e25869. [Google Scholar] [CrossRef]
- Şerb, M.D.; Wang, R.; Meven, M.; Englert, U. The whole range of hydrogen bonds in one crystal structure: Neutron diffraction and charge-density studies of N,N-dimethylbiguanidinium bis(hydrogensquarate). Acta Crystallogr. B 2011, 67, 552–559. [Google Scholar] [CrossRef]
- Wang, A.; Wang, R.; Kalf, I.; Dreier, A.; Lehmann, C.W.; Englert, U. Charge-Assisted Halogen Bonds in Halogen-Substituted Pyridinium Salts: Experimental Electron Density. Cryst. Growth Des. 2017, 17, 2357–2364. [Google Scholar] [CrossRef]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, X.; Li, X.; Meng, L.; Zheng, S. The role of molecular electrostatic potentials in the formation of a halogen bond in furan⋯XY and thiophene⋯XY complexes. ChemPhysChem 2011, 12, 1080–1087. [Google Scholar] [CrossRef]
- Chakalov, E.R.; Tupikina, E.Y.; Ivanov, D.M.; Bartashevich, E.V.; Tolstoy, P.M. The Distance between Minima of Electron Density and Electrostatic Potential as a Measure of Halogen Bond Strength. Molecules 2022, 27, 4848. [Google Scholar] [CrossRef] [PubMed]
- Lyssenko, K.A.; Nelubina, Y.V.; Safronov, D.V.; Haustova, O.I.; Kostyanovsky, R.G.; Lenev, D.A.; Antipin, M.Y. Intermolecular N3⋯N3 interactions in the crystal of pentaerythrityl tetraazide. Mendeleev Commun. 2005, 15, 232–234. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Wakisaka, A.; Ono, T.; Sonoda, T. Magnitude and origin of the attraction and directionality of the halogen bonds of the complexes of C6F5X and C6H5X (X = I, Br, Cl and F) with pyridine. Chem. Eur. J. 2012, 18, 951–960. [Google Scholar] [CrossRef]
- Forni, A.; Rendine, S.; Pieraccini, S.; Sironi, M. Solvent effect on halogen bonding: The case of the I⋯O interaction. J. Mol. Graph. Model. 2012, 38, 31–39. [Google Scholar] [CrossRef]
- Bedeković, N.; Piteša, T.; Eraković, M.; Stilinović, V.; Cinčić, D. Anticooperativity of Multiple Halogen Bonds and Its Effect on Stoichiometry of Cocrystals of Perfluorinated Iodobenzenes. Cryst. Growth Des. 2022, 22, 2644–2653. [Google Scholar] [CrossRef]





| Contact | BPL / Å | Å | Å | G / a.u. | / a.u. | V / a.u. | E / a.u. |
|---|---|---|---|---|---|---|---|
| A | 2.9120 | 0.1503 | 1.4847 | 0.01635 | 0.73 | −0.01731 | −0.00095 |
| B | 2.9352 | 0.1093 | 1.5402 | 0.01505 | 0.93 | −0.01413 | 0.00092 |
| C | 3.2461 | 0.0746 | 0.9252 | 0.00846 | 0.77 | −0.00733 | 0.00113 |
| D | 3.2720 | 0.0217 | 0.4890 | 0.00375 | 1.17 | −0.00242 | 0.00132 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Terwingen, S.; Wang, R.; Englert, U. Three for the Price of One: Concomitant I⋯N, I⋯O, and I⋯π Halogen Bonds in the Same Crystal Structure. Molecules 2022, 27, 7550. https://doi.org/10.3390/molecules27217550
van Terwingen S, Wang R, Englert U. Three for the Price of One: Concomitant I⋯N, I⋯O, and I⋯π Halogen Bonds in the Same Crystal Structure. Molecules. 2022; 27(21):7550. https://doi.org/10.3390/molecules27217550
Chicago/Turabian Stylevan Terwingen, Steven, Ruimin Wang, and Ulli Englert. 2022. "Three for the Price of One: Concomitant I⋯N, I⋯O, and I⋯π Halogen Bonds in the Same Crystal Structure" Molecules 27, no. 21: 7550. https://doi.org/10.3390/molecules27217550